




Next: Numerical examples
Up: Strong lateral variations in
Previous: Strong lateral variations in
The starting point for wavefield extrapolation algorithms is an
equation that governs the evolution of the wavefield in depth,
| 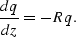 |
(50) |
The Crank-Nicolson finite-difference scheme makes a numerical
approximation of the depth derivative, by equating the two sides of
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) at a point midway between depth
steps n and n+1:
) at a point midway between depth
steps n and n+1:
| 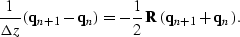 |
(51) |
Rearranging terms gives the implicit system,
| 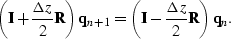 |
(52) |
An extrapolator in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will be stable if
) will be stable if
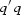 either decreases or remains constant with depth. Therefore
for stable extrapolation,
either decreases or remains constant with depth. Therefore
for stable extrapolation,
| 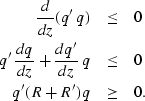 |
|
| |
| (53) |
This implies that if R+R' is symmetric non-negative definite, then
extrapolation with equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will be
unconditionally stable.
With a similar proof, Godfrey et al. (1979) showed the same condition
applies to the extrapolation matrix
) will be
unconditionally stable.
With a similar proof, Godfrey et al. (1979) showed the same condition
applies to the extrapolation matrix 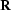 under Crank-Nicolson
extrapolation with equation (
under Crank-Nicolson
extrapolation with equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
If
).
If 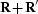 is symmetric non-negative definite, then stable
extrapolation is guaranteed.
is symmetric non-negative definite, then stable
extrapolation is guaranteed.
While the helical factorization begins with
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we really solve the implicit
system,
), we really solve the implicit
system,
| 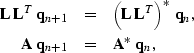 |
(54) |
| (55) |
where 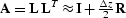 .To relate this to equation (
.To relate this to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can
premultiply that equation by an invertible matrix
), we can
premultiply that equation by an invertible matrix 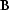 to
provide a slightly more general Crank-Nicolson extrapolation system
with the same stability requirements:
to
provide a slightly more general Crank-Nicolson extrapolation system
with the same stability requirements:
| 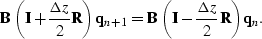 |
(56) |
Equating equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and (
)
and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) produces a formula for
) produces a formula for 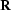 in
terms of the helical factorization,
in
terms of the helical factorization, 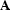 :
:
| 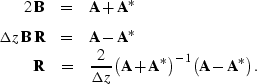 |
(57) |
| (58) |
| (59) |
Bulletproof stability requires 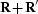 to be symmetric
non-negative definite. For the helical factorization this matrix is
given by,
to be symmetric
non-negative definite. For the helical factorization this matrix is
given by,
| 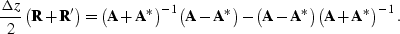 |
(60) |
In the constant velocity case, the matrix 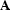 represents a
stationary filtering operation. Therefore the composite matrices,
represents a
stationary filtering operation. Therefore the composite matrices,
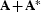 and
and 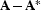 commute with
each other.
Under this scenario, the matrix
commute with
each other.
Under this scenario, the matrix 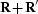 becomes the zero
matrix, which clearly satisfies the non-negative definite criterion
required for stability. Constant velocity extrapolation with
equation (
becomes the zero
matrix, which clearly satisfies the non-negative definite criterion
required for stability. Constant velocity extrapolation with
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is therefore unconditionally
stable.
) is therefore unconditionally
stable.
Unfortunately, however, if the velocity varies laterally, 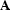 and
and 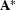 no longer commute with each other, and so the
composite matrices
no longer commute with each other, and so the
composite matrices 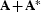 and
and 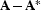 do not commute either. Consequently stable extrapolation
cannot be guaranteed.
Furthermore, there are no obvious steps we can take to ensure that
equation (
do not commute either. Consequently stable extrapolation
cannot be guaranteed.
Furthermore, there are no obvious steps we can take to ensure that
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) remains non-negative definite in areas
of strong lateral velocity variations.
In practice, equation (
) remains non-negative definite in areas
of strong lateral velocity variations.
In practice, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) does indeed
encounter stability problems in some areas.
Section
) does indeed
encounter stability problems in some areas.
Section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates this problem with
some examples.
illustrates this problem with
some examples.
Essentially the problem revolves around the fact that I factor
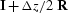 and
and
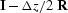 , rather than
, rather than 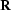 itself.
We can ensure our factorization is symmetric non-negative definite,
but not the extrapolator itself.
itself.
We can ensure our factorization is symmetric non-negative definite,
but not the extrapolator itself.





Next: Numerical examples
Up: Strong lateral variations in
Previous: Strong lateral variations in
Stanford Exploration Project
5/27/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) at a point midway between depth
steps n and n+1:
) at a point midway between depth
steps n and n+1:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will be stable if
) will be stable if
![]() either decreases or remains constant with depth. Therefore
for stable extrapolation,
either decreases or remains constant with depth. Therefore
for stable extrapolation,
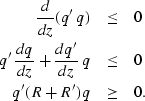
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will be
unconditionally stable.
With a similar proof, Godfrey et al. (1979) showed the same condition
applies to the extrapolation matrix
) will be
unconditionally stable.
With a similar proof, Godfrey et al. (1979) showed the same condition
applies to the extrapolation matrix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
If
).
If ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we really solve the implicit
system,
), we really solve the implicit
system,
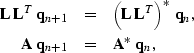
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can
premultiply that equation by an invertible matrix
), we can
premultiply that equation by an invertible matrix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and (
)
and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) produces a formula for
) produces a formula for ![]() in
terms of the helical factorization,
in
terms of the helical factorization, ![]() :
:
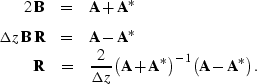
![]() to be symmetric
non-negative definite. For the helical factorization this matrix is
given by,
to be symmetric
non-negative definite. For the helical factorization this matrix is
given by,
![]() represents a
stationary filtering operation. Therefore the composite matrices,
represents a
stationary filtering operation. Therefore the composite matrices,
![]() and
and ![]() commute with
each other.
Under this scenario, the matrix
commute with
each other.
Under this scenario, the matrix ![]() becomes the zero
matrix, which clearly satisfies the non-negative definite criterion
required for stability. Constant velocity extrapolation with
equation (
becomes the zero
matrix, which clearly satisfies the non-negative definite criterion
required for stability. Constant velocity extrapolation with
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is therefore unconditionally
stable.
) is therefore unconditionally
stable.
![]() and
and ![]() no longer commute with each other, and so the
composite matrices
no longer commute with each other, and so the
composite matrices ![]() and
and ![]() do not commute either. Consequently stable extrapolation
cannot be guaranteed.
Furthermore, there are no obvious steps we can take to ensure that
equation (
do not commute either. Consequently stable extrapolation
cannot be guaranteed.
Furthermore, there are no obvious steps we can take to ensure that
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) remains non-negative definite in areas
of strong lateral velocity variations.
In practice, equation (
) remains non-negative definite in areas
of strong lateral velocity variations.
In practice, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) does indeed
encounter stability problems in some areas.
Section
) does indeed
encounter stability problems in some areas.
Section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates this problem with
some examples.
illustrates this problem with
some examples.
![]() and
and
![]() , rather than
, rather than ![]() itself.
We can ensure our factorization is symmetric non-negative definite,
but not the extrapolator itself.
itself.
We can ensure our factorization is symmetric non-negative definite,
but not the extrapolator itself.