




Next: Polynomial division
Up: Implicit extrapolation theory
Previous: Helical boundary conditions
Kolmogorov spectral factorization (reviewed in
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) provides an algorithm for
finding a minimum-phase wavelet with a desired
spectrum, or auto-correlation function.
Since positive-definite Hermitian matrices with Toeplitz
structure represent convolutions with autocorrelation functions,
Kolmogorov provides a way to efficiently decompose them into the
product of lower (causal) and upper (anti-causal) parts. Once this
LU factorization has been achieved, the two parts can be inverted
rapidly by recursion (polynomial division).
) provides an algorithm for
finding a minimum-phase wavelet with a desired
spectrum, or auto-correlation function.
Since positive-definite Hermitian matrices with Toeplitz
structure represent convolutions with autocorrelation functions,
Kolmogorov provides a way to efficiently decompose them into the
product of lower (causal) and upper (anti-causal) parts. Once this
LU factorization has been achieved, the two parts can be inverted
rapidly by recursion (polynomial division).
As with the Helmholtz equation, the complex scale-factor,  ,
means
,
means 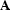 is symmetric, but not Hermitian, so the standard
Kolmogorov factorization will fail.
As discussed in Chapter
is symmetric, but not Hermitian, so the standard
Kolmogorov factorization will fail.
As discussed in Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , however, the method can
be extended to factor any cross-spectrum into a pair of minimum phase
wavelets and a delay Claerbout (1998c). The algorithm
follows the standard Kolmogorov factorization; however, negative lags
are kept separately rather than being discarded.
, however, the method can
be extended to factor any cross-spectrum into a pair of minimum phase
wavelets and a delay Claerbout (1998c). The algorithm
follows the standard Kolmogorov factorization; however, negative lags
are kept separately rather than being discarded.
The Kolmogorov factorization is not exact because the filters are
factored in the frequency domain, assuming circular boundary
conditions; while the polynomial division
is performed in the time domain with transient boundary
conditions. As a result the filters must be padded in the time-domain
before spectral factorization.
Padding does not significantly effect the overall cost of the
migration, as the computational expense lies in the polynomial
division, not in the factorization.
Alternative methods for cross-spectral factorization may avoid the
circular boundary condition problem. For example, the Wilson-Burg
algorithm Sava et al. (1998); Wilson (1969), based on Newton's recursive
linearization, can efficiently factor polynomials, and is especially
suited to the helical coordinate system.





Next: Polynomial division
Up: Implicit extrapolation theory
Previous: Helical boundary conditions
Stanford Exploration Project
5/27/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , however, the method can
be extended to factor any cross-spectrum into a pair of minimum phase
wavelets and a delay Claerbout (1998c). The algorithm
follows the standard Kolmogorov factorization; however, negative lags
are kept separately rather than being discarded.
, however, the method can
be extended to factor any cross-spectrum into a pair of minimum phase
wavelets and a delay Claerbout (1998c). The algorithm
follows the standard Kolmogorov factorization; however, negative lags
are kept separately rather than being discarded.