




Next: Introduction
Up: Spectral factorization of wavefields
Previous: Conclusions
Helical factorization of the Helmholtz
equation
In this chapter, I demonstrate how multi-dimensional spectral
factorization allows the efficient solution of constant coefficient
partial differential equations (PDE's).
I begin with the simple example of Poisson's equation: following
Claerbout (1998b), I show how the helical coordinate system
allows the factorization of the finite-difference stencil into a pair
of minimum phase filters that can be inverted rapidly by
back-substitution.
Moving to a wave propagation example, I construct a finite-difference
approximation to the Helmholtz operator in the 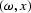 domain that describes propagation of a single frequency wave.
This filter can also be factored into a pair of of filters, and
I show these factors can act as recursive one-way wave propagators
that are accurate up to 90
domain that describes propagation of a single frequency wave.
This filter can also be factored into a pair of of filters, and
I show these factors can act as recursive one-way wave propagators
that are accurate up to 90 .
.





Next: Introduction
Up: Spectral factorization of wavefields
Previous: Conclusions
Stanford Exploration Project
5/27/2001
![]() domain that describes propagation of a single frequency wave.
This filter can also be factored into a pair of of filters, and
I show these factors can act as recursive one-way wave propagators
that are accurate up to 90
domain that describes propagation of a single frequency wave.
This filter can also be factored into a pair of of filters, and
I show these factors can act as recursive one-way wave propagators
that are accurate up to 90![]() .
.