




Next: The frequency domain approach
Up: Removing data aliasing artifacts
Previous: Removing data aliasing artifacts
The sparse solver in the time domain employs a regularization term
that enforces spikyness in the model space Nichols (1994). This approach
is well-suited for time-domain processing and makes use of
iterative solvers as opposed to direct inversion
as described in equations (14) and (15).
For instance, by choosing an approximation of the  norm
for the model space regularization, we can focus
the energy of the model vector
norm
for the model space regularization, we can focus
the energy of the model vector  into its main components.
Ulrych et al. (2000) advocate a regularization by the Cauchy-Gauss
model. In any case, the objective function to minimize becomes
into its main components.
Ulrych et al. (2000) advocate a regularization by the Cauchy-Gauss
model. In any case, the objective function to minimize becomes
| 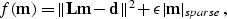 |
(17) |
where  is the
is the  norm and where |.|sparse
induces a sparse model. Iteratively reweighted least-squares
algorithms with the proper weighting function produce an artifact-free
model space Bube and Langan (1997).
A more ambitious Huber norm can be used as well
Guitton and Symes (1999) for the
norm and where |.|sparse
induces a sparse model. Iteratively reweighted least-squares
algorithms with the proper weighting function produce an artifact-free
model space Bube and Langan (1997).
A more ambitious Huber norm can be used as well
Guitton and Symes (1999) for the  case.
case.





Next: The frequency domain approach
Up: Removing data aliasing artifacts
Previous: Removing data aliasing artifacts
Stanford Exploration Project
4/29/2001