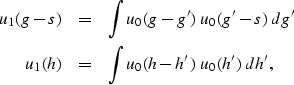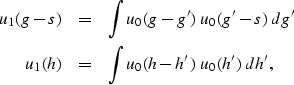One-dimensional earth and impulsive source

Let's define u₀ as the primary wavefield and u₁ the surface-related, first-order multiple wavefield recorded at the surface. If the earth varies only as a function of depth, then u will not depend on both s and g, but only on the offset, h=g-s. In this one-dimensional case, equation (10) becomes

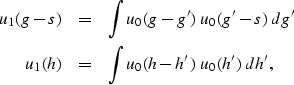$$\begin{eqnarray} u_1(g-s) & = & \int u_0(g-g') \; u_0(g'-s) \; dg' \\ u_1(h) & = & \int u_0(h-h') \; u_0(h') \; dh',\end{eqnarray}$$ (11) (12)

where h'=g'-s. Equation (12) clearly represents a convolution, so can be computed by multiplication in the Fourier domain such that

 

U₁(k_h) = U₀(k_h)²,

where U_i(k_h) is the Fourier transform of u_i(h) defined by  

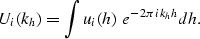$$U_i(k_h) = \int u_i(h) \; e^{-2 \pi i k_h h} dh.$$ (14)

Equation (13) can be extended to deal with a smoothly varying earth by considering common shot-gathers (or common midpoint gathers) independently, and assuming the earth is locally one-dimensional in the vicinity of the shot e.g., Rickett and Guitton (2000):

 

U₁(k_h,s) = U₀(k_h,s)².