




Next: Examples of data regularization
Up: Regularizing local plane waves
Previous: High-order plane-wave destructors
Let us denote by 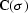 the operator of convolving the
data with the 2-D filter C(Zt,Zx) of equation (
the operator of convolving the
data with the 2-D filter C(Zt,Zx) of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
assuming the local slope
)
assuming the local slope  . In order to determine the slope,
we can define the least-squares goal
. In order to determine the slope,
we can define the least-squares goal
| 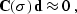 |
(110) |
where 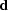 is the known data and the approximate equality
implies that the solution is found by minimizing the power of the
left-hand side. Equations (
is the known data and the approximate equality
implies that the solution is found by minimizing the power of the
left-hand side. Equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) show that
the slope
) show that
the slope  enters in the filter coefficients in an
essentially non-linear way. However, one can still apply the linear
iterative optimization methods by an analytical linearization of
equation (
enters in the filter coefficients in an
essentially non-linear way. However, one can still apply the linear
iterative optimization methods by an analytical linearization of
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The linearization (also known as the Newton
iteration) implies solving the linear system
). The linearization (also known as the Newton
iteration) implies solving the linear system
| 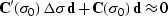 |
(111) |
for the slope increment 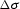 . Here
. Here 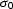 is the initial slope estimate, and
is the initial slope estimate, and 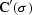 is a
convolution with the filter, obtained by differentiating the filter
coefficients of
is a
convolution with the filter, obtained by differentiating the filter
coefficients of 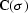 with respect to
with respect to
 . After system (
. After system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is solved, the initial
slope
) is solved, the initial
slope 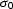 is updated by adding
is updated by adding 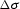 to
it, and one can solve the linear problem again. Depending on the
starting solution, the method may require several non-linear
iterations to achieve an acceptable convergence. The described
linearization approach is similar in idea to tomographic velocity
estimation Nolet (1987).
to
it, and one can solve the linear problem again. Depending on the
starting solution, the method may require several non-linear
iterations to achieve an acceptable convergence. The described
linearization approach is similar in idea to tomographic velocity
estimation Nolet (1987).
In the case of a time- and space-varying slope  ,system (
,system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) may lead to undesirably rough slope
estimates. Moreover, the solution will be undefined in regions of
unknown or constant data. Both these problems are solved by adding a
regularization (styling) goal to system (
) may lead to undesirably rough slope
estimates. Moreover, the solution will be undefined in regions of
unknown or constant data. Both these problems are solved by adding a
regularization (styling) goal to system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The
additional goal takes the form analogous to (
). The
additional goal takes the form analogous to (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
| 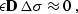 |
(112) |
where 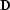 is an appropriate roughening operator and
is an appropriate roughening operator and  is a scaling coefficient. For simplicity, I chose
is a scaling coefficient. For simplicity, I chose 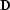 to be the
gradient operator. An alternative choice would be to treat local dips
as smooth data and to apply to them the tension-spline preconditioning
technique from the previous section.
to be the
gradient operator. An alternative choice would be to treat local dips
as smooth data and to apply to them the tension-spline preconditioning
technique from the previous section.
In theory, estimating two different slopes  and
and
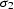 from the available data is only marginally more
complicated than estimating a single slope. The convolution operator
becomes a cascade of
from the available data is only marginally more
complicated than estimating a single slope. The convolution operator
becomes a cascade of 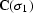 and
and
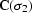 , and the linearization yields
, and the linearization yields
| 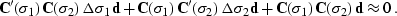 |
(113) |
The regularization condition should now be applied to both 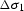 and
and 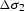 :
:
| 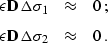 |
(114) |
| (115) |
The solution will obviously depend on the initial values of
 and
and 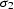 , which should not be equal to
each other. System (
, which should not be equal to
each other. System (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is generally underdetermined,
because it contains twice as many estimated parameters as equations,
but an appropriate choice of the starting solution and the additional
regularization (
) is generally underdetermined,
because it contains twice as many estimated parameters as equations,
but an appropriate choice of the starting solution and the additional
regularization (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) allow us to arrive at a
practical solution.
) allow us to arrive at a
practical solution.
The application examples of the next subsection demonstrate that when
the system of equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
or (
)
or (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are optimized in the least-squares
sense in a cycle of several linearization iterations, it leads to
smooth and reliable slope estimates. The regularization
conditions (
) are optimized in the least-squares
sense in a cycle of several linearization iterations, it leads to
smooth and reliable slope estimates. The regularization
conditions (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) assure
a smooth extrapolation of the slope to the regions of unknown or
constant data.
) assure
a smooth extrapolation of the slope to the regions of unknown or
constant data.





Next: Examples of data regularization
Up: Regularizing local plane waves
Previous: High-order plane-wave destructors
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
assuming the local slope
)
assuming the local slope ![]() the operator of convolving the
data with the 2-D filter C(Zt,Zx) of equation (
the operator of convolving the
data with the 2-D filter C(Zt,Zx) of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
assuming the local slope
)
assuming the local slope ![]() . In order to determine the slope,
we can define the least-squares goal
. In order to determine the slope,
we can define the least-squares goal
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) show that
the slope
) show that
the slope ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The linearization (also known as the Newton
iteration) implies solving the linear system
). The linearization (also known as the Newton
iteration) implies solving the linear system
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is solved, the initial
slope
) is solved, the initial
slope ![]() ,system (
,system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) may lead to undesirably rough slope
estimates. Moreover, the solution will be undefined in regions of
unknown or constant data. Both these problems are solved by adding a
regularization (styling) goal to system (
) may lead to undesirably rough slope
estimates. Moreover, the solution will be undefined in regions of
unknown or constant data. Both these problems are solved by adding a
regularization (styling) goal to system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The
additional goal takes the form analogous to (
). The
additional goal takes the form analogous to (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
![]() and
and
![]() from the available data is only marginally more
complicated than estimating a single slope. The convolution operator
becomes a cascade of
from the available data is only marginally more
complicated than estimating a single slope. The convolution operator
becomes a cascade of ![]() and
and
![]() , and the linearization yields
, and the linearization yields
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is generally underdetermined,
because it contains twice as many estimated parameters as equations,
but an appropriate choice of the starting solution and the additional
regularization (
) is generally underdetermined,
because it contains twice as many estimated parameters as equations,
but an appropriate choice of the starting solution and the additional
regularization (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) allow us to arrive at a
practical solution.
) allow us to arrive at a
practical solution.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
or (
)
or (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are optimized in the least-squares
sense in a cycle of several linearization iterations, it leads to
smooth and reliable slope estimates. The regularization
conditions (
) are optimized in the least-squares
sense in a cycle of several linearization iterations, it leads to
smooth and reliable slope estimates. The regularization
conditions (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) assure
a smooth extrapolation of the slope to the regions of unknown or
constant data.
) assure
a smooth extrapolation of the slope to the regions of unknown or
constant data.