




Next: Data regularization as an
Up: Fundamentals of data regularization
Previous: Statistical estimation
In order to understand the structure of the matrices 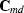 and
and 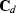 , we need to make some assumptions about the
relationship between the true model
, we need to make some assumptions about the
relationship between the true model  and the data
and the data
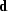 . A natural assumption is that if the model were known
exactly, the observed data would be related to it by a forward
interpolation operator
. A natural assumption is that if the model were known
exactly, the observed data would be related to it by a forward
interpolation operator 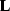 as follows:
as follows:
| 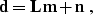 |
(4) |
where  is an additive observational noise. For simplicity,
we can assume that the noise is uncorrelated and normally distributed
around zero:
is an additive observational noise. For simplicity,
we can assume that the noise is uncorrelated and normally distributed
around zero:
| 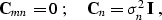 |
(5) |
where  is an identity matrix of the data size, and
is an identity matrix of the data size, and
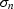 is a scalar. Assuming that there is no linear correlation
between the noise and the model, we arrive at the following
expressions for the second moment matrices in
formula (3):
is a scalar. Assuming that there is no linear correlation
between the noise and the model, we arrive at the following
expressions for the second moment matrices in
formula (3):
| 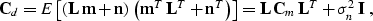 |
(6) |
| ![\begin{displaymath}
\bold{C}_{md} = E\left[\bold{m}\,
\left(\bold{m}^T\,\bold{L}^T + \bold{n}^T\right)\right] =
\bold{C}_{m}\,\bold{L}^T\;.\end{displaymath}](img29.gif) |
(7) |
Substituting equations (6) and (7) into
(3), we finally obtain the following specialized form of
the Gauss-Markoff formula:
| 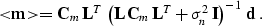 |
(8) |
Assuming that 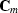 is invertible, we can also rewrite
equation (8) in a mathematically equivalent form
is invertible, we can also rewrite
equation (8) in a mathematically equivalent form
| 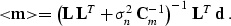 |
(9) |
The equivalence of formulas (8) and (9)
follows from the simple matrix equality
| 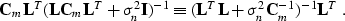 |
(10) |
It is important to note an important difference between
equations (8) and (9): The inverted matrix
has data dimensions in the first case, and model dimensions in the
second case. I discuss the practical significance of this distinction
in Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
In order to simplify the model estimation problem further, we can
introduce a local differential operator 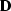 . A model
. A model  complies with the operator
complies with the operator 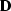 if the residual after we apply
this operator
if the residual after we apply
this operator 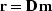 is uncorrelated and
normally distributed. This means that
is uncorrelated and
normally distributed. This means that
| ![\begin{displaymath}
E\left[\bold{D}\,\bold{m}\,\bold{m}^T\,\bold{D}^T\right] =
\bold{D}\,\bold{C}_m\,\bold{D}^T = \sigma_m^2\,\bold{I}\;,\end{displaymath}](img36.gif) |
(11) |
where the identity matrix  has the model size. Furthermore,
assuming that
has the model size. Furthermore,
assuming that 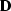 is invertible, we can represent
is invertible, we can represent 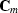 as follows:
as follows:
| 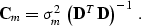 |
(12) |
Substituting formula (12) into (8) and
(9), we can finally represent the model estimate in the
following equivalent forms:
| 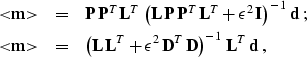 |
(13) |
| (14) |
where 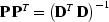 and
and 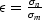 .
.
The first simplification step has now been accomplished. By
introducing additional assumptions, we have approximated the
covariance matrices 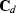 and
and 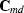 with the forward
interpolation operator
with the forward
interpolation operator 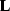 and the differential operator
and the differential operator
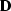 . Both
. Both 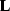 and
and 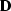 act locally on the model.
Therefore, they are sparse, efficiently computed operators. Different
examples of operators
act locally on the model.
Therefore, they are sparse, efficiently computed operators. Different
examples of operators 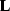 ,
,  , and
, and  are
discussed later in this dissertation. In the next section, I proceed
to the second simplification step.
are
discussed later in this dissertation. In the next section, I proceed
to the second simplification step.





Next: Data regularization as an
Up: Fundamentals of data regularization
Previous: Statistical estimation
Stanford Exploration Project
12/30/2000
![]() and
and ![]() , we need to make some assumptions about the
relationship between the true model
, we need to make some assumptions about the
relationship between the true model ![]() and the data
and the data
![]() . A natural assumption is that if the model were known
exactly, the observed data would be related to it by a forward
interpolation operator
. A natural assumption is that if the model were known
exactly, the observed data would be related to it by a forward
interpolation operator ![]() as follows:
as follows:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![]() . A model
. A model ![]() complies with the operator
complies with the operator ![]() if the residual after we apply
this operator
if the residual after we apply
this operator ![]() is uncorrelated and
normally distributed. This means that
is uncorrelated and
normally distributed. This means that
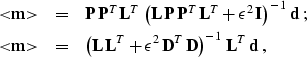
![]() and
and ![]() with the forward
interpolation operator
with the forward
interpolation operator ![]() and the differential operator
and the differential operator
![]() . Both
. Both ![]() and
and ![]() act locally on the model.
Therefore, they are sparse, efficiently computed operators. Different
examples of operators
act locally on the model.
Therefore, they are sparse, efficiently computed operators. Different
examples of operators ![]() ,
, ![]() , and
, and ![]() are
discussed later in this dissertation. In the next section, I proceed
to the second simplification step.
are
discussed later in this dissertation. In the next section, I proceed
to the second simplification step.