




Next: Preconditioning
Up: Background
Previous: Background
One method of solving
so-called ``mixed-determined'' problems is to force the problem to be purely
overdetermined by applying regularization, in which case Equation (1)
becomes
| ![\begin{displaymath}
\bf
\left[ \begin{array}
{c}
\bf B \ \epsilon \bf A
\en...
...ft[ \begin{array}
{c}
\bf d \ \bf 0
\end{array} \right].
\end{displaymath}](img10.gif) |
(3) |
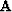 is the regularization operator; usually convolution with a compact differential filter.
is the regularization operator; usually convolution with a compact differential filter.
 is a scaling factor. The least squares inverse is then
is a scaling factor. The least squares inverse is then
| 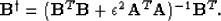 |
(4) |
The regularization term, 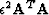 , is nonsingular with positive eigenvalues,
so it stabilizes singularities in
, is nonsingular with positive eigenvalues,
so it stabilizes singularities in 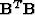 , but it is poorly-conditioned for many
common choices of
, but it is poorly-conditioned for many
common choices of 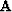 , i.e., Laplacian or gradient. The smallest eigenvalues of
, i.e., Laplacian or gradient. The smallest eigenvalues of
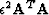 correspond to smooth (low-frequency) model components,
so iterative methods of solving equation (4), including the conjugate-direction method
used in this paper, require many iterations to obtain smooth estimates of the model Shewchuk (1994).
correspond to smooth (low-frequency) model components,
so iterative methods of solving equation (4), including the conjugate-direction method
used in this paper, require many iterations to obtain smooth estimates of the model Shewchuk (1994).





Next: Preconditioning
Up: Background
Previous: Background
Stanford Exploration Project
9/5/2000