![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
Biondo Biondi
biondo@sep.stanford.edu
Solving the one-way wave equation by using implicit finite-differences on helical boundary conditions is a computationally attractive way to avoid the operator anisotropy induced by splitting Rickett et al. (1998); Rickett (2000). The method relies on a numerical spectral factorization of a finite-difference operator into the product of two operators: one minimum phase and the other maximum phase. When the velocity is laterally constant this factorization can be efficiently and reliably performed in the Fourier domain using the Kolmogoroff method Claerbout (1976). Unfortunately, when the velocity is laterally varying the operator to be factored is non-stationary, and Kolmogoroff cannot be directly applied. Rickett describes an approximate method to address this problem 2000, but unfortunately when the velocity field is rapidly changing instability may incur.
I attempt to circumvent the problems of factoring a non-stationary operator by analytical approximating the finite-difference operator as the cascade of operators that are either causal or anti-causal. The application of such one-sided operators by implicit finite-difference (e.g. Crank-Nicolson) requires only the inversion of triangular matrices, which is quickly accomplished by back substitution (i.e. polynomial division).
I am interested to achieve wide-angle accuracy, thus I concentrate my attention on the finite-difference step of the Fourier-Finite Difference Plus Interpolation (FFDPI) method that I previously presented 2000, which, in turn, is based on the Fourier-Finite Difference (FFD) method introduced by Ristow and Ruhl 1994.
The FFDPI correction term can be written in matrix notation as
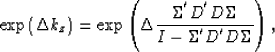 |
(1) |
If we consider the simplest case of a two terms approximation we have
| |
(2) |
Zhang et al. 2000 use a cascade similar to equation (2) together with helical boundary conditions to derive an efficient implicit finite-difference method that solves the two-dimensional one-way wave equation along the Cartesian axes and the diagonals. My goal is to employ the cascade in equation (2) together with helical boundary conditions to solve directly the three-dimensional problem, in a way similar to Rickett et al 1998. However, this note is limited to the analysis of the inaccuracies introduced by the factorization when solving the two-dimensional one-way wave equation.
Two simple approximations I will consider the following two simple approximations:
| |
(3) |
| |
(4) |
If the coefficients of ![]() and
and ![]() are constant;
i.e.,
the reference velocity and the medium velocity are
laterally invariant,
the analysis can be performed
in the wavenumber domain (k).
In the following, I will assume
that the operators are in the wavenumber-domain.
It is straightforward to verify that
are constant;
i.e.,
the reference velocity and the medium velocity are
laterally invariant,
the analysis can be performed
in the wavenumber domain (k).
In the following, I will assume
that the operators are in the wavenumber-domain.
It is straightforward to verify that
| (5) |
In contrast, it is also easy to verify that
| |
(6) |
The analytical expressions of the errors introduced by the above approximations are not particularly insightful. Therefore, I will show the errors introduced by the approximations for some concrete instances of both D and the velocities. In particular, I will show the effective phase curves corresponding to the use of each approximation and compare them with the phase curves corresponding to the application of the exact FFD correction [equation (1)], and the application of a simple split-step correction.
 |
I start by using for D
the first-order approximation of the derivative operator.
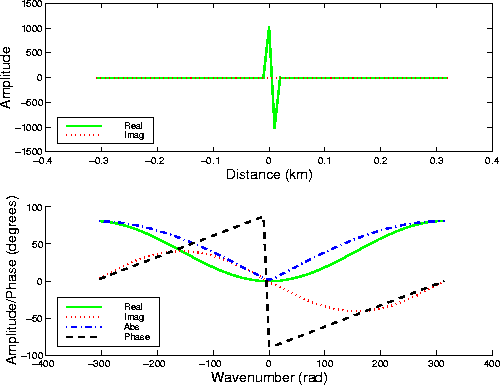
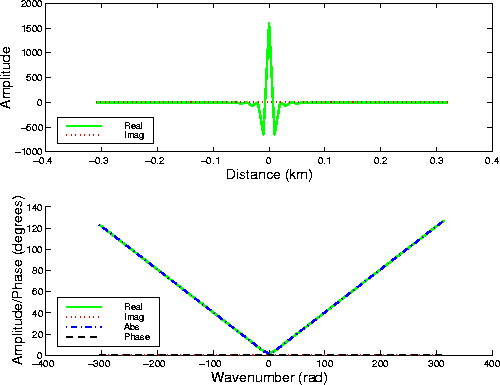
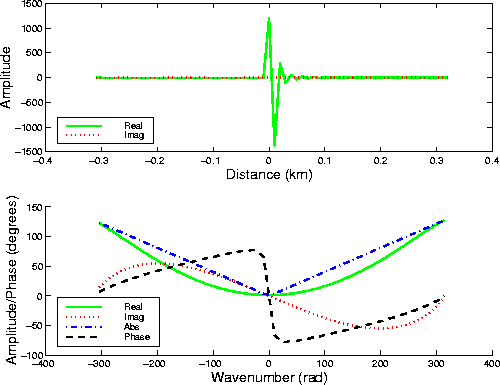
Figure 1 shows
the space-domain representation (top),
and the wavenumber-domain representation (bottom),
of D.
Notice that D ![]() .D is also minimum phase.
.D is also minimum phase.
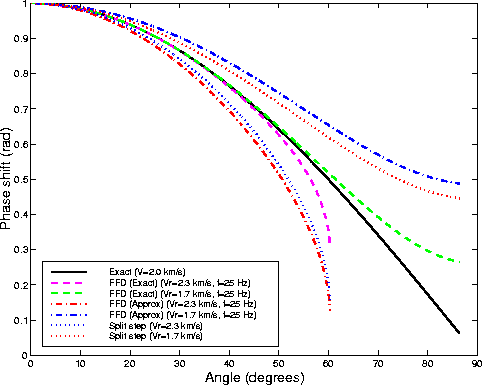
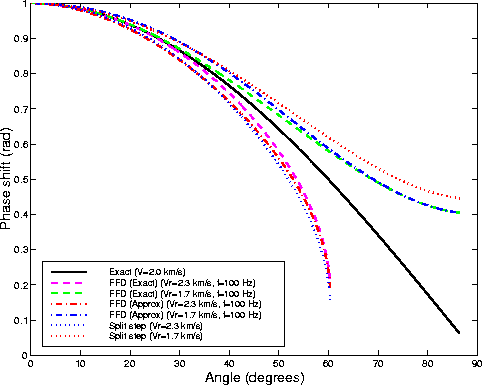
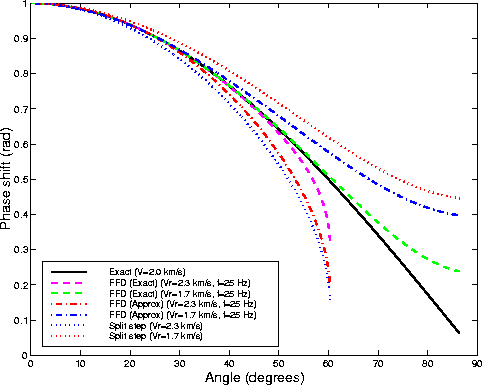
Figure 2 shows the phase curves
plotted as a function of the propagation angle.
The approximate FFD curves correspond to the
approximation of equation (3).
The phase curves were computed assuming a medium velocity of 2 km/s,
a low reference velocity of 1.7 km/s,
a high reference velocity of 2.3 km/s,
a spatial sampling rate of 10 m,
and a temporal frequency of 25 Hz.
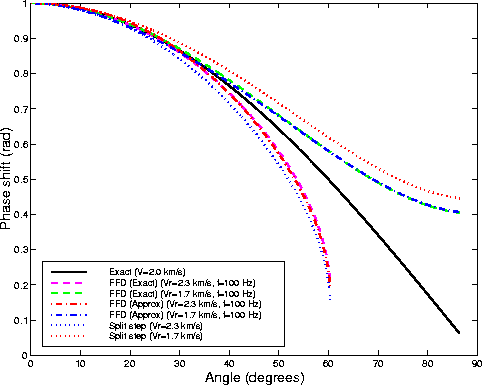
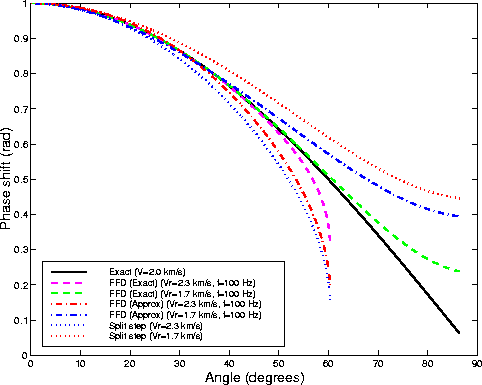
Figure 3 shows the phase curves
computed with the same parameters as in Figure 2,
with the exception of the temporal frequency,
that was set to 100 Hz.
The phase curves are
affected by the temporal frequency for two reasons:
first,
![]() is function of the wavenumber
(bottom of Figure 1);
second, the higher the temporal frequency,
the worse D'D approximates the Laplacian,
affecting the accuracy of the ``exact'' FFD correction.
The frequency of 100 Hz corresponds
to the Nyquist wavenumber for the waves propagating
at 90 degrees with velocity of 2 km/s.
From Figure 2 we can immediately
conclude that
is function of the wavenumber
(bottom of Figure 1);
second, the higher the temporal frequency,
the worse D'D approximates the Laplacian,
affecting the accuracy of the ``exact'' FFD correction.
The frequency of 100 Hz corresponds
to the Nyquist wavenumber for the waves propagating
at 90 degrees with velocity of 2 km/s.
From Figure 2 we can immediately
conclude that ![]() is a poor approximation
at low frequencies,
even worse than the simple split-step correction.
The curves corresponding to
is a poor approximation
at low frequencies,
even worse than the simple split-step correction.
The curves corresponding to ![]() and
and
![]() get closer at higher frequencies,
but mostly because
get closer at higher frequencies,
but mostly because ![]() becomes
more ineffective.
The phase errors for
becomes
more ineffective.
The phase errors for ![]() are sufficiently discouraging that I do not show
the amplitude curves; that are related to the
imaginary part of
are sufficiently discouraging that I do not show
the amplitude curves; that are related to the
imaginary part of ![]() .
.
 |
 |
In contrast,
the approximation of equation (4) is more promising,
not only because of its lack of stability problems
[equation (6)],
but because the phase errors are better behaved.
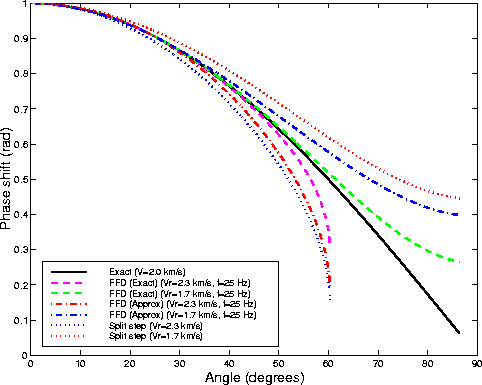
Figures 4 and 5 show
the phase curves corresponding to ![]() .At low frequency (25 Hz) the approximate FFD correction
is worse than the exact one,
but is better then the simple split-step correction
(Figure 2).
At high frequency (100 Hz),
the approximate FFD correction is very close to the exact one
(Figure 5).
.At low frequency (25 Hz) the approximate FFD correction
is worse than the exact one,
but is better then the simple split-step correction
(Figure 2).
At high frequency (100 Hz),
the approximate FFD correction is very close to the exact one
(Figure 5).
 |
 |
The final goal is to solve the 3-D one-wave equation,
not the 2-D one.
The 2-D Laplacian cannot be as easily factored analytically
as the 1-D one,
and thus I would need to rely to numerical methods
to find appropriate expressions for D.
In particular, I would need to apply Kolmogoroff factorization.
Figures 6 and 7 show the step
of such procedure for the 1-D case.
Figure 6 shows the zero-phase first derivative
operator obtained by inverse Fourier transforming
![]() .Figure 7 shows the result of Kolmogoroff
applied to the operator in Figure 6.
Notice the similarity with the operator shown in
Figure 1.
The small wiggles following the large negative spike
in the space-domain representation shown in
Figure 7 are responsible
for the difference in behavior at high wavenumbers.
.Figure 7 shows the result of Kolmogoroff
applied to the operator in Figure 6.
Notice the similarity with the operator shown in
Figure 1.
The small wiggles following the large negative spike
in the space-domain representation shown in
Figure 7 are responsible
for the difference in behavior at high wavenumbers.
 |
 |
The phase curves for this choice of D are shown in Figures 8 and 9. They are very similar to the ones shown in Figures 4 and 5, with the exception of the curves corresponding to the ``exact'' FFD correction. Because the new D is a better approximation of the derivative operator also for high wavenumber, the curves corresponding to 100 Hz are almost identical to the ones corresponding to 25 Hz.
 |
 |
Conclusions The problems encountered when factoring a non-stationary operator for applying the FFD correction with laterally varying velocity can be circumvented by approximating the exact FFD correction as the sum of terms that contains either causal or anti-causal operators.
The first approximation that I considered is unattractive both because of its phase errors and because of its potential for instability. The second approximation that I analyzed has the desired amplitude behavior and better phase properties than the first one. However, its usefulness is still undetermined by the results obtained so far. The errors introduced by these approximations should be weighted against the errors introduced by splitting, also taking into account that the splitting errors are greatly reduced in the FFDPI algorithm Biondi (2000), with respect to the simple FFD algorithm.
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)