




Next: METHOD 2: A subtraction
Up: Proposed solutions to attenuate
Previous: Proposed solutions to attenuate
Equation 7 introduces two matrices that are difficult to compute:
the data covariance matrix 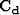 and the model covariance matrix
and the model covariance matrix
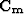 . I concentrate my efforts on the data covariance matrix only,
the computation of the model covariance matrix being beyond the scope of this
paper. When coherent noise is present in the data, residual variables
are no longer IID and the covariance matrices should not be approximated
by diagonal operators. IID residual components is equivalent to
having a residual with a white spectrum. Thus coherent noise will add ``color''
to the spectrum of the residual. The goal of the covariance matrices is
to absorb this spectrum. As Jon Claerbout 1999 asserts:
. I concentrate my efforts on the data covariance matrix only,
the computation of the model covariance matrix being beyond the scope of this
paper. When coherent noise is present in the data, residual variables
are no longer IID and the covariance matrices should not be approximated
by diagonal operators. IID residual components is equivalent to
having a residual with a white spectrum. Thus coherent noise will add ``color''
to the spectrum of the residual. The goal of the covariance matrices is
to absorb this spectrum. As Jon Claerbout 1999 asserts:
Clearly, the noise spectrum is the same as the data covariance only if
we accept the theoritician's definition that E(d)=Fm.
There is no ambiguity and no argument if we drop the word ``variance''
and use the word ``spectrum''.
This statement is the basis of the first filtering method.
It says that the experimental residuals (squared) should be
weighted inversely by their multivariate spectrum for
optimal convergence. Because a PEF whitens data from which it was estimated,
it approximates the inverse power spectrum of the data. Thus a PEF (squared)
estimated from the residual or the model accomplishes the role of the inverse covariance
matrices 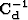 and
and 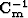 in Equation 7.
The fitting goals in Equation 9 become, omitting the regularization term,
in Equation 7.
The fitting goals in Equation 9 become, omitting the regularization term,
| 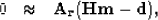 |
(10) |
where 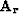 is a PEF estimated from the residual and
is a PEF estimated from the residual and 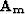 from
the unknown model.
Thanks to the Helical boundary conditions Claerbout (1998), the
PEF may be computed in more than one dimension (2-D, 3-D).
This gives us a lot of flexibility to calculate the residual spectrum.
An important task is to develop a strategy to estimate the residual PEF
from
the unknown model.
Thanks to the Helical boundary conditions Claerbout (1998), the
PEF may be computed in more than one dimension (2-D, 3-D).
This gives us a lot of flexibility to calculate the residual spectrum.
An important task is to develop a strategy to estimate the residual PEF 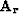 .
I propose the following algorithm:
.
I propose the following algorithm:
Algorithm1
- 1.
- Compute the current residual r = Hm - d.
- 2.
- Estimate a PEF
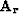 from the residual.
from the residual.
- 3.
- Minimize the objective function (l2 norm)
| 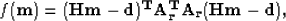 |
(11) |
- 4.
- Go to 1 after a certain number of iterations in step (3).
Notice that the first PEF is estimated from the data (if no
prior coherent noise model exists). Then the residual PEF is re-estimated
iteratively. This optimization scheme is very similar to IRLS
algorithms where weighting functions are re-computed after
a certain number of iterations. Because I re-compute the PEF
iteratively, my goal is to have the best estimate of the
residual's multivariate spectrum. This problem is then piece-wise
linear. With this strategy, the residual should be IID. Notice that
the minimization of the objective function can be done with our
favorite fast conjugate gradients method.





Next: METHOD 2: A subtraction
Up: Proposed solutions to attenuate
Previous: Proposed solutions to attenuate
Stanford Exploration Project
9/5/2000