




Next: Proposed solutions to attenuate
Up: The inverse problem
Previous: The inverse problem
The least-squares criterion comes directly from the hypothesis
that the pdf of each observable
data and each model parameter is Gaussian.
These assumptions lead to the General Discrete Inverse Problem
Tarantola (1987). Finding m is then equivalent to minimizing
the quadratic function (or objective function)
| 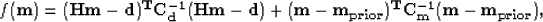 |
(6) |
where 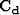 and
and 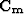 are the covariance operators, and
are the covariance operators, and
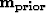 a model given a priori.
The covariance matrix
a model given a priori.
The covariance matrix 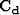 combines experimental errors and modeling
uncertainties. Modeling uncertainties describe the difference between what
the operator can predict and the data. Thus the covariance matrix
combines experimental errors and modeling
uncertainties. Modeling uncertainties describe the difference between what
the operator can predict and the data. Thus the covariance matrix 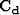 is often called the noise covariance matrix. Assuming (1) uniform variance
of the model and of the noise, (2) covariance matrices are diagonal
, i.e., uncorrelated model an data components, and (3) no prior model
is often called the noise covariance matrix. Assuming (1) uniform variance
of the model and of the noise, (2) covariance matrices are diagonal
, i.e., uncorrelated model an data components, and (3) no prior model 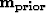 ,
the objective function becomes
,
the objective function becomes
| 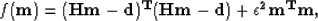 |
(7) |
where  is a function of the noise and model variances. The previous assumptions leading
to Equation 8 are quite strong when we are dealing with seismic data because the variance
of the noise/model
may be not uniform and the components of the noise/model are not independent. Minimizing
the objective function in Equation 8 is equivalent to having the two
fitting goals for m
is a function of the noise and model variances. The previous assumptions leading
to Equation 8 are quite strong when we are dealing with seismic data because the variance
of the noise/model
may be not uniform and the components of the noise/model are not independent. Minimizing
the objective function in Equation 8 is equivalent to having the two
fitting goals for m
| 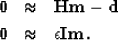 |
(8) |
| (9) |
The first inequality expresses the need for the operator H
to fit the input data 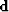 .The second inequality is often called the regularization (or model styling) term.
The minimization of Equation 9, when the operator H is linear,
may be done using any kind of linear method such as the steepest descent algorithm or
faster conjugate gradients/directions methods Paige and Saunders (1982). From now on,
I will refer to Equation 9 as the ``simplest'' approach.
When the assumptions leading to Equation 9 are respected, the convergence
towards m is easy to achieve. In particular, the components of the residual
.The second inequality is often called the regularization (or model styling) term.
The minimization of Equation 9, when the operator H is linear,
may be done using any kind of linear method such as the steepest descent algorithm or
faster conjugate gradients/directions methods Paige and Saunders (1982). From now on,
I will refer to Equation 9 as the ``simplest'' approach.
When the assumptions leading to Equation 9 are respected, the convergence
towards m is easy to achieve. In particular, the components of the residual
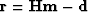 become IID. This IID property implies that no
coherent information is left in the residual and that each variable of the residual
has similar intensity (or power). The main factor that may alter this property is the
presence of noise in the data that violates assumptions about both the uniform distribution and
the need of independent noise components.
become IID. This IID property implies that no
coherent information is left in the residual and that each variable of the residual
has similar intensity (or power). The main factor that may alter this property is the
presence of noise in the data that violates assumptions about both the uniform distribution and
the need of independent noise components.





Next: Proposed solutions to attenuate
Up: The inverse problem
Previous: The inverse problem
Stanford Exploration Project
9/5/2000