Angle-domain common-image gathers are representations of the seismic images sorted by the aperture angle at the reflection point Fomel and Prucha (1999); Prucha et al. (1999a). In the space-domain, the reflection angles can be evaluated by the simple differential equation:
![]()
|
rays
Figure 1 The geometrical relationship relating the reflection angle | 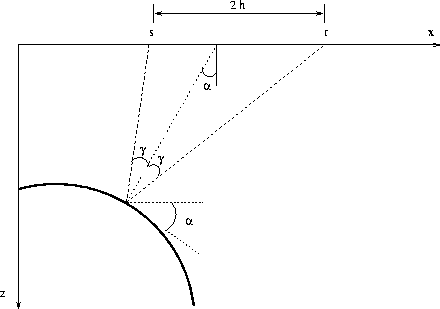 |
Prucha et al. (1999a) evaluate wave-equation angle-domain
common-image gathers (ADCIG) by slant-stacking between the downward
continuation and the imaging steps. They also produce their output as
a function of offset ray-parameter (p) instead of the reflection
angle (![]() ). However, angle-domain gathers do not need to be computed
by slant stacks directly, but could be more easily evaluated in the
Fourier-domain, with output in the true reflection angle, using the
simple equation:
). However, angle-domain gathers do not need to be computed
by slant stacks directly, but could be more easily evaluated in the
Fourier-domain, with output in the true reflection angle, using the
simple equation:
| |
(1) |
It is interesting to emphasize that this Fourier-domain method of computation of angle-gathers is a radial-trace transform. Ottolini (1982) shows that slant stacks are, in fact, generally equivalent to radial-trace transforms, with significant advantages and disadvantages for each of these two alternatives.
In this paper, we review the radial stretch theory and show that computing the ADCIGs using equation (1) is indeed equivalent to slant stacks but that it gives us the freedom to postpone the conversion to angle until after prestack wave-equation migration. This Fourier domain method makes it possible to convert seismic images easily from the offset-domain to the angle-domain without re-migrating the data.
The novelty of our method is that, in the Fourier-domain, the radial-trace transformation can be easily regularized, thus leading to smooth and continuous representations of the reflectors along the angle axis. A similar method of regularized stretch has been used in other applications: velocity continuation Fomel (1998), Stolt migration Vaillant and Fomel (1999), and Stolt residual migration Sava (1999a,b). It could also find many other applications, for example in coherent-noise removal using radial-trace transforms Brown and Claerbout (2000).
Our method of angle-gather computation is different from the slant-stack approach not only in the domain in which it operates, but also in the low cost involved, the robustness, and simplicity of the implementation. If we compute angle-gathers in conjunction with Stolt residual migration, this method becomes even more attractive since the seismic images are already transformed to the Fourier-domain, which makes the true cost of the transformation insignificant.