Hybrid l¹-l² function

The hybrid l¹-l² norm has been widely used in geophysics Bube and Langan (1997); Fomel and Claerbout (1995); Nichols (1994). It is generally solved using iteratively reweighted least-squares (IRLS) algorithms with an appropriate weighting matrix. These algorithms have proved efficient but are also acknowledged to be difficult to tune. As an alternative to using IRLS algorithms to compute the hybrid l¹-l² norm, Claerbout (1996) introduced the Huber norm Huber (1973). This norm is a patching of the l¹ norm for high residuals and of the l² norm for small residuals:

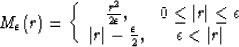$$M_{\epsilon}(r) = \left\{ \begin{array} {cc} \frac{r^2}{2\ep... ...frac{\epsilon}{2}, & \epsilon < \vert r\vert \end{array}\right.$$ (4)

where r is the residual. We call $\sum_{i=1}^N\,M_{\epsilon}(r_i)$ the Huber misfit function, or the Huber function, for short (Figure 2). Note that the Huber function is smooth near zero residual and weights small residuals by the mean square. It is reasonable to suppose that the Huber function, while maintaining robustness against large residuals, is easier to minimize than l¹. The parameter $\epsilon$, which controls the limit between l¹ and l², is called the Huber threshold.

 

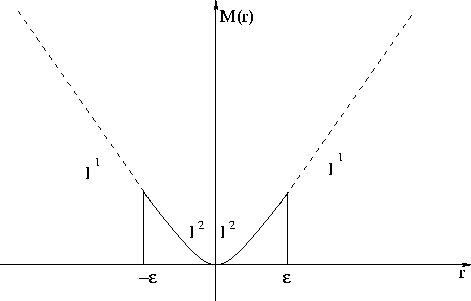
huber Figure 2 Error measure proposed by Huber (1973). The upper part above $\epsilon$ is the l1 norm, while the lower part is the l2 norm.

The implementation of an inverse solver to minimize the Huber function is quite challenging and leads to innovative non-linear algorithms in geophysics Guitton (2000b). To summarize, I developed a quasi-Newton method with a line search. I implemented a More and Thuente Line Search More and Thuente (1994) algorithm, which ensures a sufficient decrease in the objective function f (equation 3) and obeys curvature conditions (the so-called Wolfe conditions, Kelley (1999)). The update of the Hessian is made using a Limited Memory BFGS method as proposed by Nocedal (1980) and Liu and Nocedal (1989). This method is guaranteed to converge to a minimum. This strategy has proved efficient in solving the Huber problem correctly Guitton and Symes (1999); Guitton (2000a) and eliminates the restart parameter encountered in IRLS algorithms, which makes this Huber solver easier to use.