Practice

The half-derivative filter belongs to a family of filters known as rho filters. Past attempts Lumley (1994) to apply these filters to a CG inversion have exhibited divergence after the first few iterations, despite the fact that CG iteration should never diverge when the operator is linear and the gradient is non-zero. Nevertheless, I attempted CG inversion of the system:

 

$$d\;=\;{\bf HV}m\;\;\mbox{\rm ,}$$ (5)

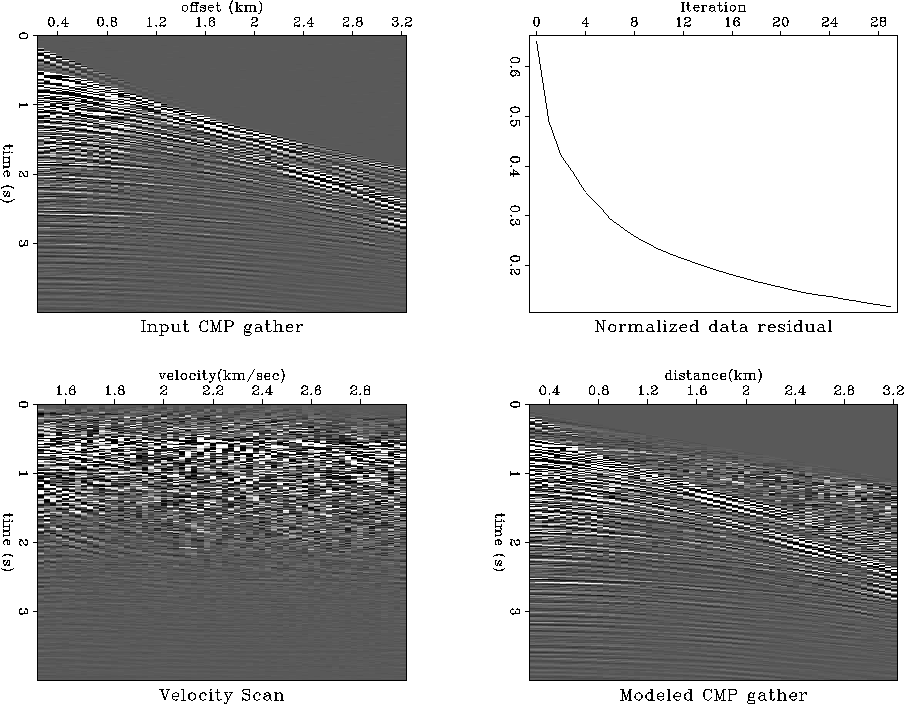
where d= data, H= half-derivative filter, V= velocity transform operator, and m= model. This was applied to the CMP gathers seen in Figures 2 (synthetic) and 1 (real). These two figures also both show the residuals converging, the velocity scans resulting from the CG iterations, and the forward-modeled data.

 

real.vel
Figure 1 Top left: Real CMP gather. Top right: Residual power versus iteration. Bottom left: Representation of CMP gather in velocity space. Bottom right: Inversion of bottom left.

 

elf.vel
Figure 2 Top left: Synthetic CMP gather. Top Right: Residual power versus iteration. Bottom left: Representation of CMP gather in velocity space. Bottom right: Inversion of bottom left.

In an attempt to improve the rate of convergence, I re-ordered the equation as:

 

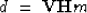$$d\;=\;{\bf VH}m$$ (6)

This also allowed convergence. Figures 3 and 4 show the convergence rate of the second system (6) to be better than that of the first system (5) and both of these are superior to the convergence speed for the trial with no half-derivative filter.

 

elf.residual-compare
Figure 3 Comparison of rates of convergence for the synthetic data. While there is relatively little difference in the magnitudes of the final residuals, the two best rates are obtained with the half-derivative filter.

 

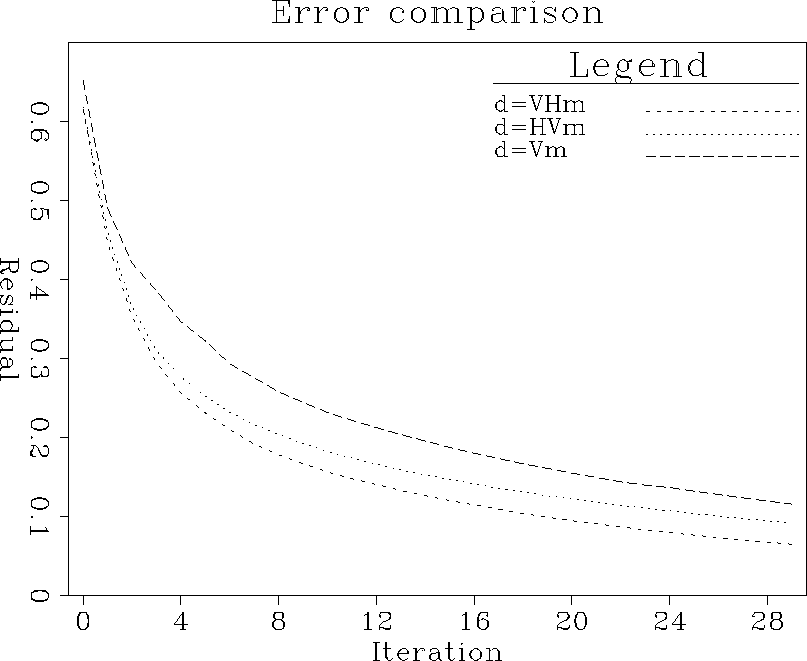
real.residual-compare
Figure 4 Comparison of rates of convergence for the real data. The best rate is obtained for the system d=VHm.

It is interesting to note that the residuals decrease more and the half-derivative filter has a greater effect for the real CMP gather than for the synthetic CMP gather. This is most likely a result of dispersion from the finite-difference method used to create the synthetic data.