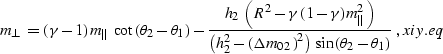Next: 2D AMO operator
Up: Derivation of integral AMO
Previous: AMO amplitudes
Cascading DMO and inverse DMO allowed us to evaluate the
summation path of AMO and the corresponding weighting
function.
However, this procedure is not sufficient for evaluating the third major
component of the integral operator, that is, its aperture (range of
integration). To solve this problem, Fomel and Biondi 1995c
applied an alternative approach by
defining AMO as the cascade of 3D common-offset common-azimuth
migration and 3D modeling at a different azimuth and offset.
I birefly discuss their derivations in this appendix as part of
a complete definition of integral AMO.
The impulse response of the common-offset common-azimuth migration is a
symmetric ellipsoid with the center in the input midpoint and axis of
symmetry along the input-offset direction. Such an ellipsoid is
described by the general formula
| 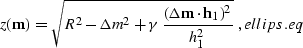 |
(90) |
where z stands for the depth coordinate, 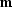 is the surface
coordinate,
is the surface
coordinate, 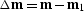 , R is the small semi-axis of the
ellipsoid, and
, R is the small semi-axis of the
ellipsoid, and 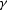 is a nondimensional parameter describing the
stretching of the ellipse
is a nondimensional parameter describing the
stretching of the ellipse 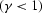 . Deregowski and Rocca
1981 derived the following connections
between the geometric properties of the reflector and the coordinates
of the corresponding impulse in the data:
. Deregowski and Rocca
1981 derived the following connections
between the geometric properties of the reflector and the coordinates
of the corresponding impulse in the data:
| 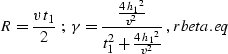 |
(91) |
where v is the propagation velocity.
The impulse response of the AMO operator corresponds kinematically
to the reflections from the ellipsoid defined by
equation ellips.eq to a different azimuth and different
offset.
To constrain the AMO aperture, Fomel and Biondi 1995c
based their derivations on answering the
following question: For a given elliptic
reflector defined by the input midpoint, offset, and time coordinates,
what points on the surface can form a source-receiver pair valid for a
reflection? If a point in the output midpoint-offset space cannot be
related to a reflection pattern, it should be excluded from the AMO
aperture.
Fermat's principle provides a general method of solving the kinematic
reflection problem Goldin (1986). The formal expression for the
two-point reflection traveltime is given by
| 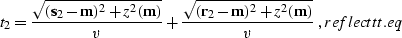 |
(92) |
where 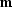 is the vertical projection of the reflection point to the
surface,
is the vertical projection of the reflection point to the
surface, 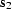 is the source location, and
is the source location, and 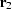 is the receiver
location for the output trace. According to Fermat's principle, the
reflection raypath between two fixed points must correspond to the
extremum value of the traveltime. Hence, in the vicinity of a
reflected ray,
is the receiver
location for the output trace. According to Fermat's principle, the
reflection raypath between two fixed points must correspond to the
extremum value of the traveltime. Hence, in the vicinity of a
reflected ray,
| 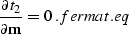 |
(93) |
Solving equation fermat.eq for 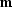 allows us to find the
reflection raypath for a given source-receiver pair on the surface.
allows us to find the
reflection raypath for a given source-receiver pair on the surface.
To find the solution of fermat.eq, it is convenient to
decompose the reflection-point projection 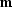 into three components:
into three components:
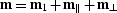 , where
, where 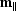 is parallel to the
input offset vector
is parallel to the
input offset vector 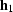 , and
, and 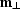 is perpendicular to
is perpendicular to
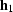 . The plane, drawn through the reflection point and the
central line of ellipsoid ellips.eq, must contain the
zero-offset (normally reflected) ray because of the cylindrical
symmetry of the reflector. The fact that the zero-offset ray is normal
to the reflector gives us the following connection between the
zero-offset midpoint
. The plane, drawn through the reflection point and the
central line of ellipsoid ellips.eq, must contain the
zero-offset (normally reflected) ray because of the cylindrical
symmetry of the reflector. The fact that the zero-offset ray is normal
to the reflector gives us the following connection between the
zero-offset midpoint 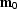 and the
and the 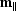 component of the
reflection point
component of the
reflection point 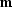 :
:
| 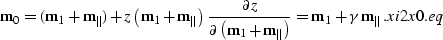 |
(94) |
Equation xi2x0.eq evaluates 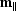 in terms of
in terms of 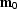 , as
follows:
, as
follows:
| 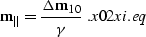 |
(95) |
where the length of the vector 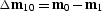 can be
determined using the following geometric connection between any given input and
output midpoints
can be
determined using the following geometric connection between any given input and
output midpoints 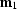 and
and 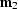 , and azimuths
, and azimuths 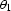 and
and
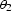
| 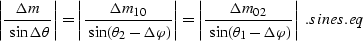 |
(96) |
To find the third component of the reflection point projection
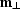 , we substitute expression x02xi.eq
into reflecttt.eq. Choosing a convenient parameterization
, we substitute expression x02xi.eq
into reflecttt.eq. Choosing a convenient parameterization
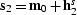 ,
, 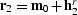 , where
, where
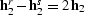 , and
, and
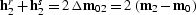 ,
we can rewrite the two-point
traveltime function from reflecttt.eq in the form
,
we can rewrite the two-point
traveltime function from reflecttt.eq in the form
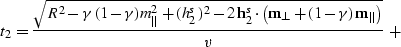
| 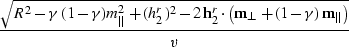 |
(97) |
Fermat's principle fermat.eq leads to a simple linear equation
for the length of 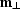 , which has the explicit solution
, which has the explicit solution
| 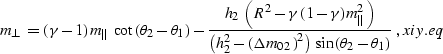 |
(98) |
where 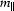 is defined by x02xi.eq, and
is defined by x02xi.eq, and 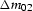 satisfies the relationship sines.eq.
satisfies the relationship sines.eq.
Because the reflection point is contained inside the ellipsoid,
its projection obeys the evident inequality
| 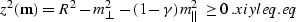 |
(99) |
It is inequality xiyleq.eq that defines the aperture of the
AMO operator.
After transformation transform and algebraic
simplifications, it takes the form of inequality t2leq.eq,
which is convenient for an efficient implementation of AMO.





Next: 2D AMO operator
Up: Derivation of integral AMO
Previous: AMO amplitudes
Stanford Exploration Project
1/18/2001
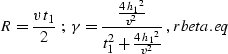
![]() into three components:
into three components:
![]() , where
, where ![]() is parallel to the
input offset vector
is parallel to the
input offset vector ![]() , and
, and ![]() is perpendicular to
is perpendicular to
![]() . The plane, drawn through the reflection point and the
central line of ellipsoid ellips.eq, must contain the
zero-offset (normally reflected) ray because of the cylindrical
symmetry of the reflector. The fact that the zero-offset ray is normal
to the reflector gives us the following connection between the
zero-offset midpoint
. The plane, drawn through the reflection point and the
central line of ellipsoid ellips.eq, must contain the
zero-offset (normally reflected) ray because of the cylindrical
symmetry of the reflector. The fact that the zero-offset ray is normal
to the reflector gives us the following connection between the
zero-offset midpoint ![]() and the
and the ![]() component of the
reflection point
component of the
reflection point ![]() :
:
![]() , we substitute expression x02xi.eq
into reflecttt.eq. Choosing a convenient parameterization
, we substitute expression x02xi.eq
into reflecttt.eq. Choosing a convenient parameterization
![]() ,
, ![]() , where
, where
![]() , and
, and
![]() ,
we can rewrite the two-point
traveltime function from reflecttt.eq in the form
,
we can rewrite the two-point
traveltime function from reflecttt.eq in the form
![]()