To derive an expression for the amplitudes of the AMO
impulse response, we start from the general
expression for the stationary-phase approximation
of the ![]() integral in equation amo_freq.eq as in
Bleistein and Handelsman (1975),
integral in equation amo_freq.eq as in
Bleistein and Handelsman (1975),
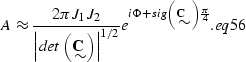 |
(81) |
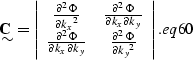 |
(82) |
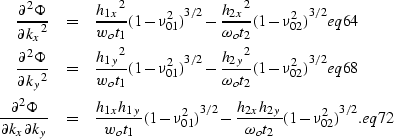 |
(83) | |
| (84) | ||
| (85) |
With a little algebra, one may verify that the determinant of the curvature matrix is
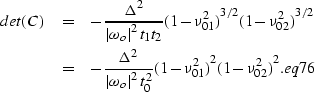 |
||
| (86) |
To obtain expressions for the AMO amplitude, we need to substitute equation eq76 in equation eq56, together with the corresponding expressions for J1 and J2. Given a forward DMO with a Jacobian term J1, I showed in Chapter 3 of the main text that an asymptotic inverse provides a better representation for the inverse DMO operator than the approximate adjoint. Also, by restricting the definition of ``true-amplitude'' to preserving the peak amplitude of reflection events, I also showed that an amplitude-preserving function for AMO can be defined by cascading Zhang and Black 1988 DMO with its asymptotic ``true-inverse''; therefore given
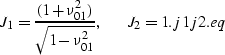 |
(87) |
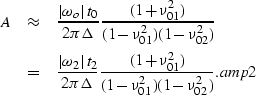 |
(88) | |
| (89) |
The expression for the amplitudes presented
in equation amo_amp.eq of the main text
follows by simple substitution of
the expressions for ![]() ,
, ![]() ,and
,and ![]() , from equations eq40, eq44 and eq48
into equation amp2.
, from equations eq40, eq44 and eq48
into equation amp2.