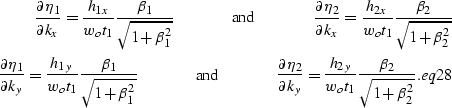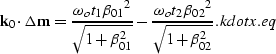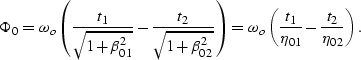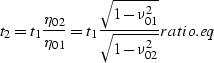Next: AMO amplitudes
Up: Derivation of integral AMO
Previous: Derivation of integral AMO
To derive a time-space representation of the AMO impulse response
from its frequency-wavenumber representation,
we evaluate the stationary-phase approximation of
the inverse Fourier transform along the midpoint coordinates.
The 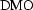 operator and its inverse,
operator and its inverse, 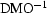 , can be
defined in the zero-offset frequency
, can be
defined in the zero-offset frequency 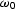 and the midpoint wavenumber
and the midpoint wavenumber 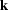 as
as
| 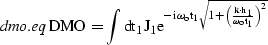 |
(63) |
| 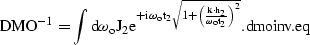 |
(64) |
The 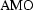 operator is given by the cascades
of
operator is given by the cascades
of 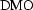 and
and 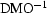 and its impulse response can
be written as,
and its impulse response can
be written as,
| 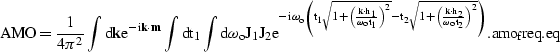 |
(65) |
The derivation of the stationary-phase approximation of the
integral in 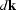 is similar to the one presented in
Black et al. (1993b) for deriving a time-space formulation
for the conventional DMO impulse response.
We begin by changing the order of the integrals
and rewriting amo_freq.eq as
is similar to the one presented in
Black et al. (1993b) for deriving a time-space formulation
for the conventional DMO impulse response.
We begin by changing the order of the integrals
and rewriting amo_freq.eq as
| ![\begin{eqnarray}
\rm AMO& =&\frac{1}{4\pi^2} \int dt_1 \int d\omega_o \int d{{\b...
... \Delta m}} \right]}\;. \nonumber \\ \EQNLABEL{amo_freq_change.eq}\end{eqnarray}](img158.gif) |
|
| (66) |
The phase of this integral is,
| 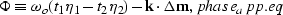 |
(67) |
where,
| 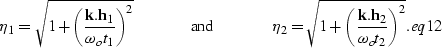 |
(68) |
Next we make the following change of variables and let
| 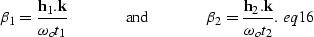 |
(69) |
Therefore, 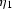 and
and 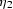 become
become
| 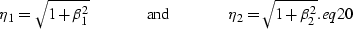 |
(70) |
The derivatives of 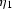 and
and 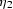 with respect to the
in-line component of the wavenumber kx
and the cross-line component ky can be written as
with respect to the
in-line component of the wavenumber kx
and the cross-line component ky can be written as
| 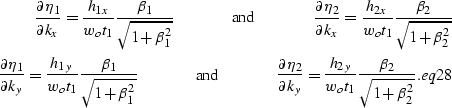 |
|
| (71) |
Making one more change of variables, we let
| 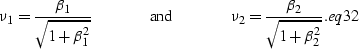 |
(72) |
Setting the derivative of the phase  to zero yields the system
of equations:
to zero yields the system
of equations:
| 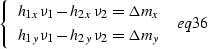 |
(73) |
which we solve for 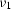 and
and 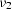 (i.e.,
(i.e., 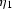 and
and 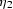 )
at the stationary
path
)
at the stationary
path 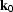 . The determinant of the system is given by
. The determinant of the system is given by
| 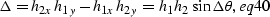 |
(74) |
and the solutions for 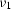 and
and 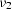 are
are
| 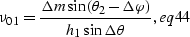 |
(75) |
and
| 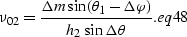 |
(76) |
Now we need to evaluate the phase function  along
the stationary path
along
the stationary path 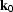 .By respectively multiplying the equations in eq36 by
k0x and k0y and summing them together we obtain,
.By respectively multiplying the equations in eq36 by
k0x and k0y and summing them together we obtain,
| 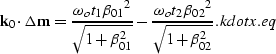 |
(77) |
Substituting this relationship into the expression of the phase
function [equation phase_app.eq] we obtain
| 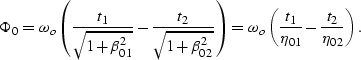 |
(78) |
The phase function along the stationary path is thus
peaked for
| 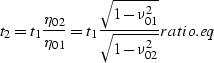 |
(79) |
Substituting equations eq44 and eq48
into ratio.eq we obtain amo_surf.eq
of the main text:
| 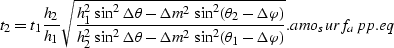 |
(80) |





Next: AMO amplitudes
Up: Derivation of integral AMO
Previous: Derivation of integral AMO
Stanford Exploration Project
1/18/2001
![]() operator and its inverse,
operator and its inverse, ![]() , can be
defined in the zero-offset frequency
, can be
defined in the zero-offset frequency ![]() and the midpoint wavenumber
and the midpoint wavenumber ![]() as
as
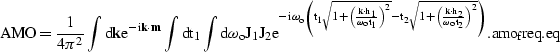
![\begin{eqnarray}
\rm AMO& =&\frac{1}{4\pi^2} \int dt_1 \int d\omega_o \int d{{\b...
... \Delta m}} \right]}\;. \nonumber \\ \EQNLABEL{amo_freq_change.eq}\end{eqnarray}](img158.gif)