




Next: AMO amplitudes
Up: Derivation of AMO
Previous: AMO impulse response
Although the expression for the kinematics of AMO is velocity independent,
the aperture of the operator depends strongly on velocity.
The domain of influence of the AMO operator is defined by the region
of validity of expression amo_surf.eq,
which becomes singular when either of the
following conditions is fulfilled:
| 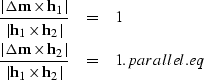 |
|
| (2) |
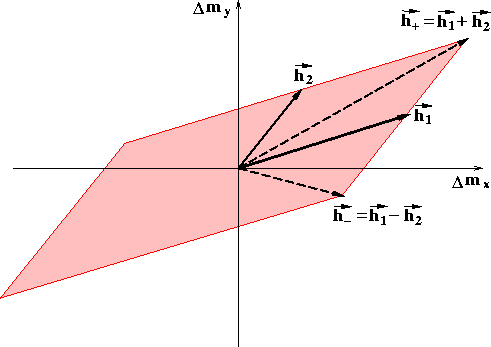
Geometrically, this means that the support
of the AMO operator at the recording surface
is limited to the region within the parallelogram
with s main diagonal 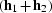 and minor diagonal
and minor diagonal
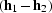 . The shaded area in
Figure amoapert shows a sample parallelogram
that represents the maximum possible spatial extent of the AMO
operator. More stringent bounds for the AMO aperture were presented by
Biondi et. al. 1998.
For given
. The shaded area in
Figure amoapert shows a sample parallelogram
that represents the maximum possible spatial extent of the AMO
operator. More stringent bounds for the AMO aperture were presented by
Biondi et. al. 1998.
For given 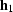 and
and 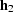 , these bounds
are a function of the input traveltime and the minimum velocity Vmin.
The parallelogram in Figure amoapert therefore represents the extreme
case where either the velocity or the input traveltime is equal to
zero. Figure impulse-small shows the effective AMO
impulse response for a limited aperture
corresponding to a realistic minimum velocity of 2
, these bounds
are a function of the input traveltime and the minimum velocity Vmin.
The parallelogram in Figure amoapert therefore represents the extreme
case where either the velocity or the input traveltime is equal to
zero. Figure impulse-small shows the effective AMO
impulse response for a limited aperture
corresponding to a realistic minimum velocity of 2 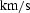 .Figure impulse-small is significantly narrower than the
whole impulse response shown in Figure impulse-big.
This velocity-dependent aperture limitation is important for an
efficient use of AMO and makes the cost of applying
AMO to the data negligible compared to the cost of
full 3-D prestack migration.
amoapert
.Figure impulse-small is significantly narrower than the
whole impulse response shown in Figure impulse-big.
This velocity-dependent aperture limitation is important for an
efficient use of AMO and makes the cost of applying
AMO to the data negligible compared to the cost of
full 3-D prestack migration.
amoapert
Figure 2 The maximum spatial support of the AMO operator (shaded parallelogram)
in the midpoint plane (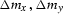 ),
as a function of the input offset
),
as a function of the input offset 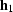 ,and the output offset
,and the output offset 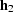 .
.
 impulse-small
impulse-small
Figure 3 The effective AMO impulse response
when
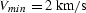 ,
and
,
and
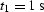 ,
,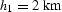 ,
,
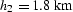 ,
,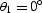 ,
,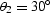 ,as in Figure 1.
,as in Figure 1.

The effective aperture becomes tiny when the azimuth rotation
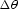 is small. At the limit, the expression in
equation amo_surf.eq is singular when the azimuth rotation
vanishes and the AMO surface reduces to a 2-D line. This operator,
corresponding to the case of offset continuation
Bolondi et al. (1984), has been derived independently by Biondi and
Chemingui 1994, Stovas and Fomel
1996, and (in a different form) Bagaini et
al. 1994. Its expression is given by the
following quadric equation,
is small. At the limit, the expression in
equation amo_surf.eq is singular when the azimuth rotation
vanishes and the AMO surface reduces to a 2-D line. This operator,
corresponding to the case of offset continuation
Bolondi et al. (1984), has been derived independently by Biondi and
Chemingui 1994, Stovas and Fomel
1996, and (in a different form) Bagaini et
al. 1994. Its expression is given by the
following quadric equation,
| ![\begin{eqnarray}
\lefteqn{{t}_{2}(\Delta m,h_{1},h_{2},{t}_{1})=} \nonumber \\ &...
...m^2]}}}
{\sqrt{2}h_{2}} & h_{2}\leq h_{1}.
\EQNLABEL{same_azim.eq}\end{eqnarray}](img25.gif) |
|
| |
| (3) |
Taking into account the effective aperture of the AMO operator,
it can be shown Fomel and Biondi (1995a) that the 3-D
operator monotonously shrinks to a line, and the limit of the
kinematics of the 3-D operator [equation amo_surf.eq]
approaches the 2-D operator [equation same_azim.eq].





Next: AMO amplitudes
Up: Derivation of AMO
Previous: AMO impulse response
Stanford Exploration Project
1/18/2001
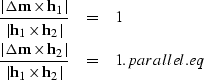
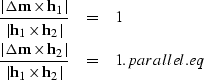

![]() is small. At the limit, the expression in
equation amo_surf.eq is singular when the azimuth rotation
vanishes and the AMO surface reduces to a 2-D line. This operator,
corresponding to the case of offset continuation
Bolondi et al. (1984), has been derived independently by Biondi and
Chemingui 1994, Stovas and Fomel
1996, and (in a different form) Bagaini et
al. 1994. Its expression is given by the
following quadric equation,
is small. At the limit, the expression in
equation amo_surf.eq is singular when the azimuth rotation
vanishes and the AMO surface reduces to a 2-D line. This operator,
corresponding to the case of offset continuation
Bolondi et al. (1984), has been derived independently by Biondi and
Chemingui 1994, Stovas and Fomel
1996, and (in a different form) Bagaini et
al. 1994. Its expression is given by the
following quadric equation,
![\begin{eqnarray}
\lefteqn{{t}_{2}(\Delta m,h_{1},h_{2},{t}_{1})=} \nonumber \\ &...
...m^2]}}}
{\sqrt{2}h_{2}} & h_{2}\leq h_{1}.
\EQNLABEL{same_azim.eq}\end{eqnarray}](img25.gif)