 |
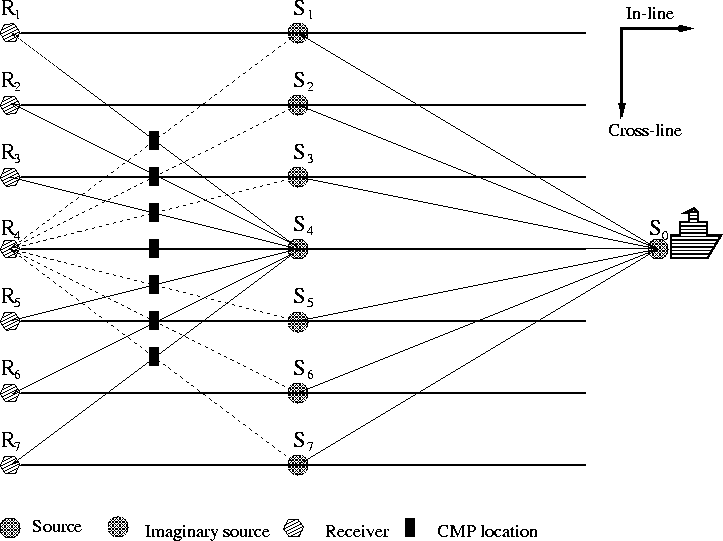
Figure 1 A multi-streamer geometry. The
In order to better understand the approach, let's assume that we have a multi-streamer acquisition system, as shown in Figure 1, with one shotline and seven streamers. Supposing that we want to predict the multiple from source S0 to receiver R4, we need to consider the contributions from all the possible multiple reflection points between S0 and R4 by cross-convolution. For instance, we need to collect all the traces with sources located at Si (i=1,...,7) and a receiver located at R4. In Figure 1, the thin solid line represents the corresponding trace collected in the survey, and the thin dashed line stands for a missing trace in the survey. The challenge is to find appropriate proxies for such missing traces.
 |
There is one well-known geophysical concept that can help us meet the challenge, the common-midpoint (CMP), which assumes that traces with the same CMP location and the same offset contain the same information about one location in the earth. Although the common-midpoint assumption is a first-order approximation when the structure is not strictly flat, I will demonstrate that it is useful in our search for the substitute traces.
For example, for the virtual trace ![]() ,the real trace
,the real trace ![]() shares the same CMP
location and has the same offset as well. The only difference is the
azimuth angle. Therefore, trace
shares the same CMP
location and has the same offset as well. The only difference is the
azimuth angle. Therefore, trace ![]() is a proxy for trace
is a proxy for trace ![]() in the multiple
prediction, with first-order accuracy. Similarly, we can find substitutes
for other virtual traces.
in the multiple
prediction, with first-order accuracy. Similarly, we can find substitutes
for other virtual traces.
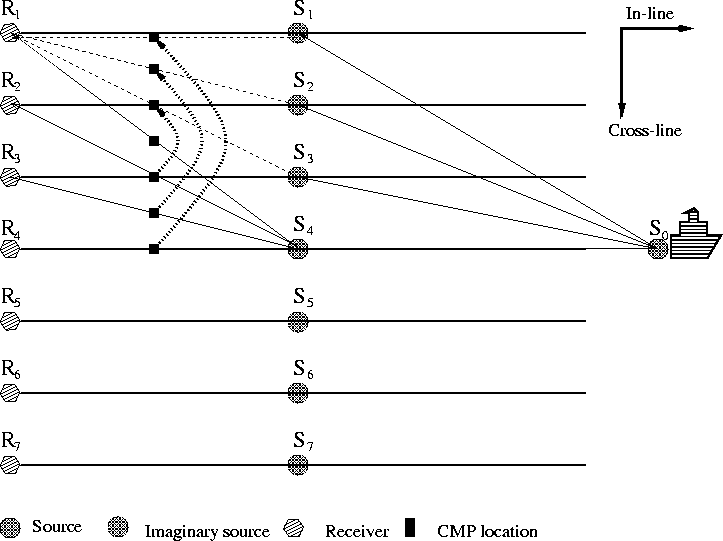
The central streamer in Figure 1 is a special case, in which we can always find substitute traces for the virtual ones with the same CMP location and offset. When we try to predict other streamers' multiple reflections, though, as in Figure 2, we are not so lucky to find proxies with the same CMP location and offset. However, we can relax the definition of a substitute trace by giving up the requirement that the proxy share the same CMP location. Then we can find another group of proxies for the missing traces, as Figure 2 illustrates. Since the cross-line spreading aperture is usually smaller than the in-line aperture, this extension may be acceptable in many real applications.
 |
There are some limitations to the method discussed in this paper. Before
addressing those limitations, I would first classify the surface multiple
reflections into two categories. Figure 3 depicts
two types of geometries for the surface multiples,
![]() and
and
![]() . The difference between these two
categories is that, source S0, surface multiple reflection position M1,
and receiver R1 are aligned together on the surface; whereas S0, M2,
and R2 can not be aligned together. The embedded physical reason is that,
multiple
. The difference between these two
categories is that, source S0, surface multiple reflection position M1,
and receiver R1 are aligned together on the surface; whereas S0, M2,
and R2 can not be aligned together. The embedded physical reason is that,
multiple ![]() is mainly caused by 1-D
earth's structures or in-line dip reflectors (2.5-D), and multiple
is mainly caused by 1-D
earth's structures or in-line dip reflectors (2.5-D), and multiple
![]() by cross-line dips or scattering
reflectors.
by cross-line dips or scattering
reflectors.
The definition of proxies in my proposal guarantees that the method in
this paper is fully applicable to the multiples like
![]() without kinematic approximations.
The approximation errors occur only when we deal with the multiples like
without kinematic approximations.
The approximation errors occur only when we deal with the multiples like
![]() . In other words, when there are
strong cross-line dips or scattering reflectors, my approach will introduce
the approximation errors inevitably.
. In other words, when there are
strong cross-line dips or scattering reflectors, my approach will introduce
the approximation errors inevitably.
|
multiple-type
Figure 3 Two types of surface multiples. | 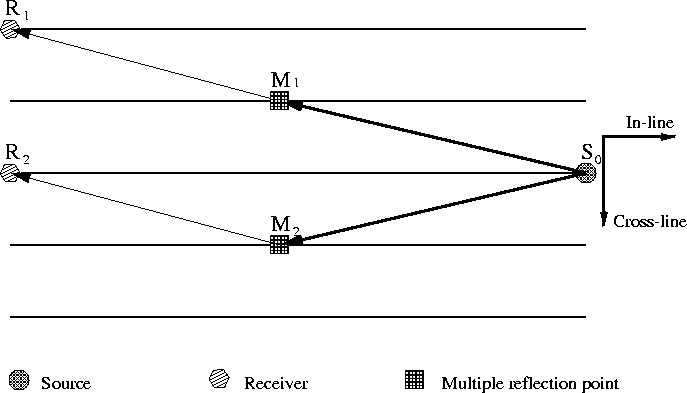 |