Marine data usually contain in-line offsets up to 3-5km, and only show a narrow range of offsets in the cross-line direction. For standard common-azimuth migration, AMO is used to rotate the data to zero cross-line offset. What we do now is use AMO to regularize the acquisition but organize data along several near-zero cross-line offsets. Strictly speaking, the data are not ``common-azimuth'', but ``quasi-common-azimuth'' or ``narrow-azimuth'' since we have only a narrow range of cross-line offsets.
These narrow-azimuth data ![]() are downward-continued as before, with an important difference in the phase of the integrand:
are downward-continued as before, with an important difference in the phase of the integrand:
 |
||
| (5) | ||
![\begin{eqnarray}
\mbox{Down}(\omega,\bold k_m,k_{hx},z) & = & \sqrt{\frac{2\pi}{...
....1in]
\phi & = & DSR(\omega,\bold k_m,\bold k_h,z) dz + k_{hy} h_y\end{eqnarray}](img19.gif) |
||
| (6) |
In 2-D, for the case of a phase-shift migration in which the equations are similar to ours, Alkhalifah 1997 found that solving for the minimum of the phase ![]() involves a sixth-order polynomial, making it difficult to find an analytical expression of the stationary path. Thus, since we are unable to use such an analytical expression for non-zero hy, we instead use only a range of values of
involves a sixth-order polynomial, making it difficult to find an analytical expression of the stationary path. Thus, since we are unable to use such an analytical expression for non-zero hy, we instead use only a range of values of ![]() centered around the stationary path
centered around the stationary path ![]() , which is given by equation (4), at zero cross-line offset. At each
, which is given by equation (4), at zero cross-line offset. At each ![]() , a different phase shift is applied: the data
, a different phase shift is applied: the data ![]() are transformed by modulation and FFT along the cross-line offset axis into
are transformed by modulation and FFT along the cross-line offset axis into ![]() , in which the range of the coordinate khy is centered around
, in which the range of the coordinate khy is centered around ![]() . Then we apply the phase shift,
. Then we apply the phase shift, ![]() , for each value of the set
, for each value of the set ![]() .
.
The reformulation of the problem has some interesting geometrical consequences. In the case of standard common-azimuth migration, the stationary path of phase ![]() derived in equation (4) is equivalent to the following relationship between the ray parameters Biondi (1998):
derived in equation (4) is equivalent to the following relationship between the ray parameters Biondi (1998):
| |
(7) |
|
ray-comaz
Figure 3 Schematic showing the ray geometry for common-azimuth downward continuation. | 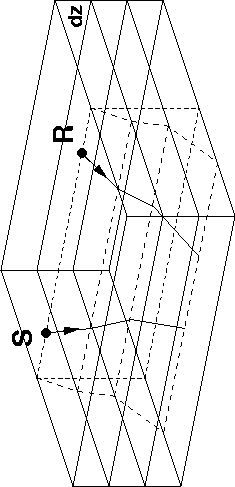 |
Equation (7) constrains the source ray and the receiver ray to lie on the same plane between depths z and z+dz, so that the sources and receivers at the new depth are aligned along the same azimuth as at the preceding depth (Figure 3). Assuming this constraint, common-azimuth migration is not strictly correct even in the simple case of a v(z) medium (Figure 4). Since the projections of the source and receiver rays on a cross-line plane do not coincide unless the angles ![]() and
and ![]() are equal, azimuth is not conserved at each depth step of downward continuation. As a general consequence, local variations in velocity, which cause ray bending phenomena, introduce an error in the computation of the common-azimuth downward continuation. Biondi and Palacharla 1996 put forward that this error is small, but by using several discrete values of khy in a neighborhood of
are equal, azimuth is not conserved at each depth step of downward continuation. As a general consequence, local variations in velocity, which cause ray bending phenomena, introduce an error in the computation of the common-azimuth downward continuation. Biondi and Palacharla 1996 put forward that this error is small, but by using several discrete values of khy in a neighborhood of ![]() , we hope to improve the result.
, we hope to improve the result.
|
ray-vofz
Figure 4 Schematic showing the ray geometry for common-azimuth downward continuation in a simple v(z) velocity model. The projections of both rays on a cross-line plane do not coincide due to non-conservation of azimuth at each depth level. | 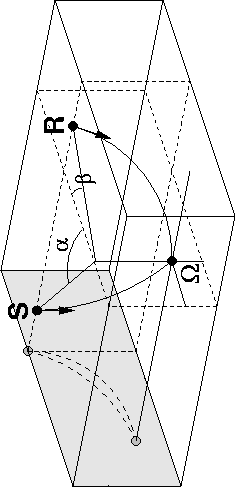 |
The narrow-azimuth approach may improve the imaging process by better taking velocity variations into account (Figure 5). Lateral velocity variations, for example, can make rays bend in the cross-line direction, and even make rays start in different planes before they converge to a deeper reflection point. The bending due to real 3-D structures is implicitly eliminated when strictly zero-azimuth data are downward continued, whereas we would like to keep it for an extension of common-azimuth migration.
|
ray-extended
Figure 5 Schematic showing the ray geometry for narrow-azimuth downward continuation. A larger range of cross-line offsets will allow the modeling of lateral variations in the velocity model by taking into consideration rays not lying in the same slanted plane. | 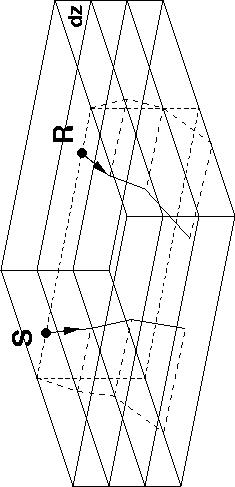 |
Our approximation, using a neighborhood of ![]() , is valid if the stationary path,
, is valid if the stationary path, ![]() , varies slowly with hy around the analytical solution,
, varies slowly with hy around the analytical solution, ![]() . To estimate these variations, we can use the Implicit Function theorem: the equation
. To estimate these variations, we can use the Implicit Function theorem: the equation ![]() , which gives the stationary path
, which gives the stationary path ![]() , also defines a relation of the general form F(khy,hy)=0. Thus, in a neighborhood of the solution
, also defines a relation of the general form F(khy,hy)=0. Thus, in a neighborhood of the solution ![]() , we use a function khy(hy), whose variations are determined by the inverse of the phase second derivative:
, we use a function khy(hy), whose variations are determined by the inverse of the phase second derivative:
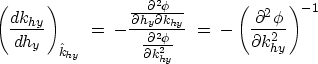 |
(8) |
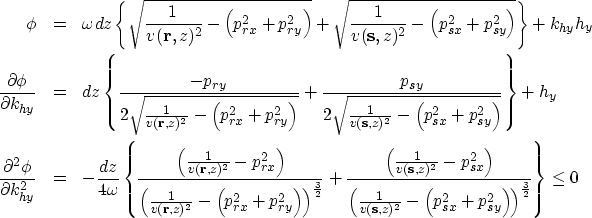 |
(9) | |
| (10) | ||
| (11) |
According to equation (6), the computation process will blow up if the second derivative becomes close to zero. The failure happens for (and only for) ![]() , corresponding to the quasi-horizontal propagation of evanescent waves. We also see that the second derivative is independent from the value of the cross-line offset, hy. This means that the variations of khy with hy, given by equation (8), will be the same around each stationary point.
, corresponding to the quasi-horizontal propagation of evanescent waves. We also see that the second derivative is independent from the value of the cross-line offset, hy. This means that the variations of khy with hy, given by equation (8), will be the same around each stationary point.
Ideally, we would like to have small variations of the stationary path with hy, in order to use correctly values of khy around the known solution ![]() for the stationary points
for the stationary points ![]() , which we cannot determine analytically. Small variations mean a high value of the phase second derivative in equation (11). When the derivative is close to zero, problems in the computation may arise, but this will never happen for waves propagating downward. The ``limiting'' case is horizontal propagation. It means that narrow-azimuth migration may not completely overcome the steep-dip limitations of common-azimuth migration.
, which we cannot determine analytically. Small variations mean a high value of the phase second derivative in equation (11). When the derivative is close to zero, problems in the computation may arise, but this will never happen for waves propagating downward. The ``limiting'' case is horizontal propagation. It means that narrow-azimuth migration may not completely overcome the steep-dip limitations of common-azimuth migration.