If we consider the perturbation in the wavefield at the surface, we can recursively downward continue it, adding at every depth step the scattered wavefield:
| |
(4) |
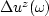 is the perturbation in the wavefield generated by the
perturbation in velocity and downward continued from the surface, and
is the perturbation in the wavefield generated by the
perturbation in velocity and downward continued from the surface, and
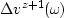 represents the scattered wavefield caused at depth
level z+1 by the perturbation in velocity from depth level z.
represents the scattered wavefield caused at depth
level z+1 by the perturbation in velocity from depth level z.
In the first-order Born approximation, the scattered wavefield can be written as
| |
(5) |
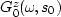 is the scattering operator at depth z,
is the scattering operator at depth z,
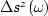 is the perturbation in slowness at depth z, and
is the perturbation in slowness at depth z, and
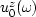 is the background wavefield at depth z.
is the background wavefield at depth z.
If we introduce equation (5) into (4) we find that
| |
(6) |
As for the background image, the perturbation in image (![]() ),
caused by the perturbation in slowness, is obtained by a summation
over all the frequencies
),
caused by the perturbation in slowness, is obtained by a summation
over all the frequencies ![]() :
:
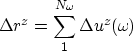 |
(7) |