




Next: Control
Up: HOW TO SMOOTH RADIALLY
Previous: HOW TO SMOOTH RADIALLY
The basic idea in building a steering filter is to create a filter
that destroys a given slope p. Further, we would like to
keep differences of the bandwidth response
for filters oriented at different
slopes to a minimum. We can achieve both these goals by constructing
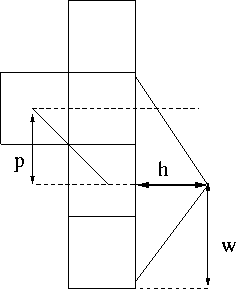
a triangle centered at the appropriate slope (Figure 6.)
Every grid
cell center which the triangle passes through is assigned a negative value
proportional to the height of the triangle at that location.
The wider the triangle base, the less precise, and more Gaussian-like
our smoother becomes, Figure 7. By decreasing the sum
of the coefficients (with a hard limit of -1 to ensure filter stability
when applying polynomial division Claerbout (1976)), we can spread information
larger distances.
steering
Figure 6 A finite-difference star for a monoplane rejection filter.
The left column contains a `1'. The right column contains
samples off a triangle.
The desired
slope is represented by p, the smaller w the more precise
the dip smoothed, and the larger h the bigger the
area the smoother acts on.
|
|  |






Next: Control
Up: HOW TO SMOOTH RADIALLY
Previous: HOW TO SMOOTH RADIALLY
Stanford Exploration Project
4/20/1999
