|
saltnew-color
Figure 1 3-D representation of the SEG-EAGE salt model. | 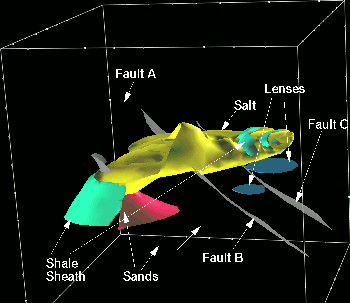 |
Kirchhoff migration methods often fail to produce satisfactory images of subsalt reflectors because they do not handle correctly multipathing of the reflected energy. When the wavefield is severely distorted by a salt body, or other complex velocity structure, the computation of the multivalued Green functions required by Kirchhoff methods is challenging. Further, even if we were able to compute the Green functions accurately and efficiently, the numerical integration of the wavefield over patchy and multivalued integration surfaces would be a difficult, and probably unreliable, task.
Wave-equation methods are an attractive and robust alternative to the complexities involved in extending Kirchhoff migration to handle correctly multipathing. However, full wave-equation 3-D prestack migration is still too computationally intensive to become a practical tool. Therefore, in the past few years I developed common-azimuth migration that is an approximation to full wave-equation 3-D prestack migration Biondi and Palacharla (1996); Biondi (1997). It exploits the narrow-azimuth nature of marine data to reduce the computational cost by a large factor (20 to 50) with respect to full wave-equation 3-D prestack migration.
I applied common-azimuth migration to the narrow-azimuth subset of SEG-EAGE salt model Aminzadeh et al. (1996) (known as C3 Narrow-Azimuth classic data set C3-NA 1997) and compared the results with the results produced by a single-arrival Kirchhoff migration. The data were recorded on the realistic and complex salt-dome structure shown in Figure 1.
|
saltnew-color
Figure 1 3-D representation of the SEG-EAGE salt model. |  |
In the subsalt areas, common-azimuth migration resolves the reflectors better than Kirchhoff migration, and yields an image with much less artifacts and spurious reflectors. The run times of common-azimuth migration and Kirchhoff migration were roughly the same. These results confirm the potentiality of wave-equation migration and give new impulse to our efforts to develop a complete wave-equation imaging (migration and velocity analysis) procedure for both structural and stratigraphic imaging.
The lack of a simple and reliable method to extract prestack information from the results of wave-equation migration has been correctly perceived as a serious drawback Etgen (1998). It curtailed the usefulness of wave-equation migration for both velocity estimation and Amplitude Versus Angle (AVA) analysis. In Prucha et al. 1999, we show a very simple method to overcome this problem. We slant stack the downward continued wavefield at each depth level and produce high-quality Common Image Gathers (CIG) that display image amplitude as a function of the reflection angle. Sinha and Biondi 1999 discuss an example that compares wave-equation CIGs with the corresponding Kirchhoff CIGs for AVA analysis. Wave-equation CIGs can also be used for estimating migration velocity in a way similar to the common use of Kirchhoff-derived CIGs. Wave-equation CIGs are sensitive to migration velocity errors as the CIG obtained by migrating offset plane waves Mosher et al. (1997); Ottolini and Claerbout (1984). However, they are more accurate because they are based on a wavefield decomposition at depth and not at the surface.
Our ultimate goal is to build a complete and self-consistent wave-equation imaging procedure. An indispensable component of wave-equation imaging is a Wave-Equation Migration Velocity Analysis (WEMVA) method. Biondi and Sava 1999 present a WEMVA based on the linearization and inversion of downward continuation operators. WEMVA is more robust and stable than conventional ray-based MVAs because it can easily handle discontinuous velocity function and multipathing. The capability of performing both velocity analysis and AVA analysis by wave-equation methods is attractive because it opens the possibility, though still far from being reality, to perform AVA analysis in more complex areas than is possible today. For AVA analysis in complex areas, wave-equation methods have a crucial advantage over asymptotic methods; they can model correctly the amplitudes variations related to the focusing and defocusing of bandlimited wavefields caused by velocity variations.
The results that are presented in this paper also show that Kirchhoff migration produced better images than common-azimuth migration in some areas of the model. At the moment of writing, it is not clear whether the degradation of the common-azimuth migration images was caused by the limitations of the numerical method employed to implement common-azimuth migration, or, by the inherent limitations of the common-azimuth migration method itself. Further investigation is needed. Common-azimuth migration has inherent limitations that are directly related to the approximations needed for its derivation and can be explained by a theoretical analysis Biondi and Palacharla (1996). Vaillant and Biondi 1999 discuss a promising method, dubbed narrow-azimuth migration, to overcome these limitations. The new method is more expensive than common-azimuth migration but it is still an order of magnitude cheaper than full wave-equation migration.