




Next: The shape of the
Up: PREDICTION-ERROR FILTER OUTPUT IS
Previous: PEF whiteness proof in
A well-known property (see FGDP or PVI)
of a 1-D PEF is that its energy clusters immediately after the
impulse at zero delay time.
Applying this idea to
the helix in Figure hlxsergey-helix
shows us that we can consider a 2-D PEF
to be a small halfplane like
hlx2dpef
with an impulse along a side.
These shapes are what we see here in
Figure 2.
whitepruf
Figure 2
A 2-D whitening filter template, and itself lagged.
At output locations ``A'' and ``B,'' the filter coefficient
is constrained to be ``1''.
When the semicircles are viewed as having infinite radius,
the B filter is contained in the A filter.
Because the output at A is orthogonal to all its inputs,
which include all inputs of B,
the output at A is orthogonal to the output of B.
|
| 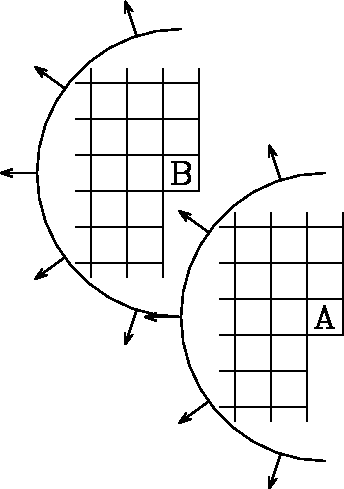 |





Figure 2 shows the input plane with a 2-D filter on top
of it at two possible locations.
The filter shape is a semidisk,
which you should imagine being of
infinitely large radius.
Notice that semidisk A includes all the points in B.
The output of disk A will be shown to be orthogonal to the output
of disk B.
Conventional least squares theory says that the coefficients of the filter
are designed so that the output of the filter
is orthogonal to each of the inputs to that filter
(except for the input under the ``1,''
because any nonzero signal cannot be orthogonal to itself).
Recall that if a given signal is orthogonal to each in a given group of signals,
then the given signal is orthogonal
to all linear combinations within that group.
The output at B is a linear combination of members
of its input group,
which is included in the input group of A,
which are already orthogonal to A.
Therefore the output at B is orthogonal to the output at A.
In summary,
| residual |
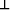 |
fitting function |
| output at A |
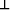 |
each input to A |
| output at A |
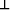 |
each input to B |
| output at A |
 |
linear combination of each input to B |
| output at A |
 |
output at B |
The essential meaning is that
a particular lag of the output autocorrelation function vanishes.
Study Figure 2 to see for what lags
all the elements of the B filter are wholly contained in the A filter.
These are the lags
where we have shown the output autocorrelation to be vanishing.
Notice another set of lags where we have proven nothing
(where B is moved to the right of A).
Autocorrelations are centrosymmetric,
which means that the value at any lag
is the same as the value at the negative of that lag,
even in 2-D and 3-D where the lag is a vector quantity.
Above we have shown that a halfplane of autocorrelation values vanishes.
By the centrosymmetry, the other half must vanish too.
Thus the autocorrelation of the PEF output is an impulse function,
so its 2-D spectrum is white.
The helix tells us why the proper filter form
is not a square with the ``1'' on the corner.
Before I discovered the helix, I understood it another way
(that I learned from John P. Burg):
For a spectrum to be white,
all
nonzero autocorrelation lags must be zero-valued.
If the filter were a quarter-plane,
then the symmetry of autocorrelations
would only give us vanishing in another quarter,
so there would be two remaining quarter-planes
where the autocorrelation was not zero.
Fundamentally,
the white-output theorem requires a
one-dimensional ordering to the values in a plane or volume,
and the same filter must apply no matter where it is applied.
Additionally, the filter must contain a halfplane of values
so that symmetry gives the other half.
It seems that we could design whitening autoregression filters
for 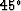 rotations,
and we could also design them for hexagonal coordinate systems.
rotations,
and we could also design them for hexagonal coordinate systems.





Next: The shape of the
Up: PREDICTION-ERROR FILTER OUTPUT IS
Previous: PEF whiteness proof in
Stanford Exploration Project
2/27/1998
