Next: Nearest-neighbor normal moveout (NMO)
Up: FAMILIAR OPERATORS
Previous: Backsolving, polynomial division and
The simplest way to eliminate low frequency noise is
to take a time derivative.
A disadvantage is that the signal changes
at high frequencies from a pulse to a doublet.
Here we look at a slightly more complicated
low-cut filter which preserves the wave shape at high frequencies
and also has an adjustable parameter
for choosing the bandwidth of the low cut.
A low-cut filter is one that removes from X
the zero frequency 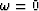 component,
and suppresses low frequency components in the output Y.
component,
and suppresses low frequency components in the output Y.
| 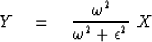 |
(24) |
To exercise various popular notations we rewrite this as
| 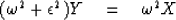 |
(25) |
Recalling the fact that the negative of a second derivative operator
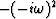 corresponds to convolution with the coefficients (-1,2,-1)
we can express the same thought using a convolution notation
corresponds to convolution with the coefficients (-1,2,-1)
we can express the same thought using a convolution notation
|  |
(26) |
which you can think of as a convolution matrix equation where both sides
have tridiagonal matrices.
We can express the same thought in Z-transform notation as
| 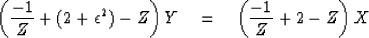 |
(27) |
and we can factor the polynomials
| 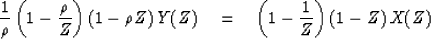 |
(28) |
where 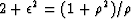 .(Factoring the polynomial amounts to factoring tridiagonal
matrices into a product of upper and lower bidiagonal matrices.)
We can group the causal filter parts together
thereby defining a causal operator polynomial ratio H(Z):
.(Factoring the polynomial amounts to factoring tridiagonal
matrices into a product of upper and lower bidiagonal matrices.)
We can group the causal filter parts together
thereby defining a causal operator polynomial ratio H(Z):
| 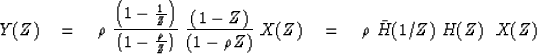 |
(29) |
Here 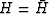 because the filter coefficients are not complex numbers.
H(Z) is called a causal filter because it uses past values
of the filter inputs to create the output.
Likewise H(1/Z) is called anticausal because the present output
comes from future inputs.
If you filter with both,
because the filter coefficients are not complex numbers.
H(Z) is called a causal filter because it uses past values
of the filter inputs to create the output.
Likewise H(1/Z) is called anticausal because the present output
comes from future inputs.
If you filter with both,
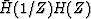 ,the filter response is
,the filter response is
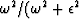 (to the extent that a time derivate is the same as a finite difference).
(to the extent that a time derivate is the same as a finite difference).
For any application
we have a choice between a symmetrical filter 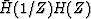 whose
amplitude response is
whose
amplitude response is 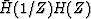 ,or the causal filter H(Z) whose
energy response is
,or the causal filter H(Z) whose
energy response is 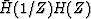 .The causal filter
.The causal filter
| 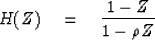 |
(30) |
obviously kills zero frequency because of the time derivative (1-Z).
The denominator 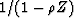 looks like the response of leaky integration.
The combination of numerator and denominator
has an impulse response that is a positive impulse,
followed by a damped exponential of negative polarity.
The area of the pulse equals the area of the damped exponential,
assuring that the zero-frequency response vanishes
and the high-frequency response is an impulse,
i.e. it does not distort high frequencies.
looks like the response of leaky integration.
The combination of numerator and denominator
has an impulse response that is a positive impulse,
followed by a damped exponential of negative polarity.
The area of the pulse equals the area of the damped exponential,
assuring that the zero-frequency response vanishes
and the high-frequency response is an impulse,
i.e. it does not distort high frequencies.
EXERCISES:
-
Give an analytic expression for
the waveform of equation (30).
-
Define a low-pass filter as 1-H(Z).
What is the low-pass impulse response?
-
Put Galilee data on a coarse mesh.
Consider north-south lines as one-dimensional signals.
Find the value of
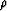 for which H is the most pleasing filter.
for which H is the most pleasing filter.
-
Find the value of
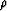 for which
for which 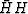 is the most pleasing filter.
is the most pleasing filter.
-
Find the value of
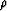 for which H applied to Galilee has minimum energy.
(Experiment with a range of about ten values around your favorite value.)
for which H applied to Galilee has minimum energy.
(Experiment with a range of about ten values around your favorite value.)
-
Find the value of
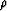 for which
for which 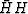 applied to Galilee has minimum energy.
applied to Galilee has minimum energy.
-
Repeat above for east-west lines.
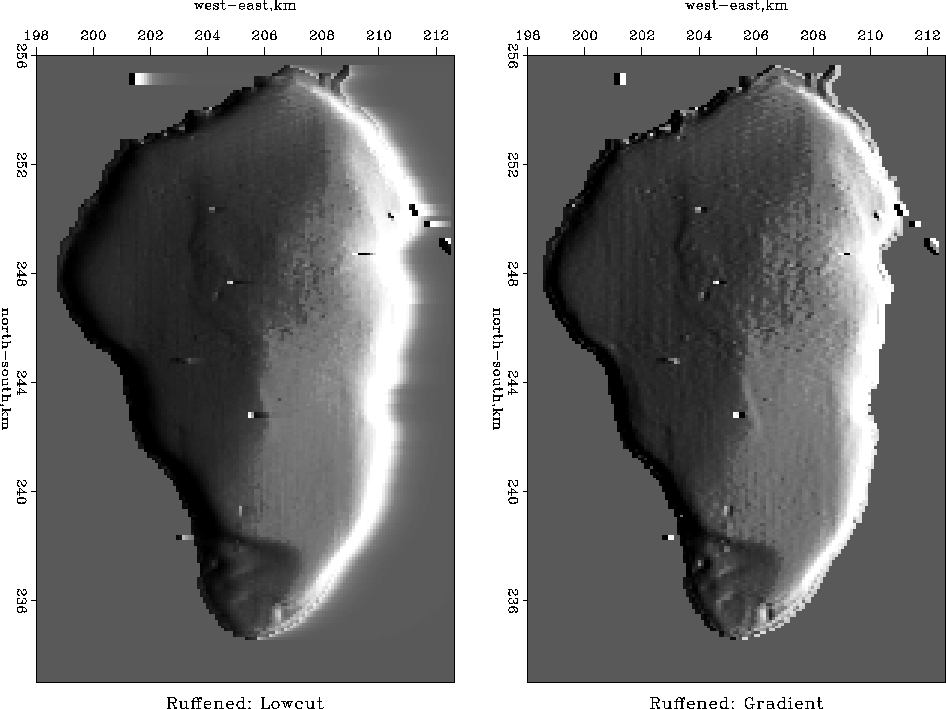
galocut90
Figure 6
The depth of the Sea of Galilee after roughening.










Next: Nearest-neighbor normal moveout (NMO)
Up: FAMILIAR OPERATORS
Previous: Backsolving, polynomial division and
Stanford Exploration Project
2/27/1998
![]() component,
and suppresses low frequency components in the output Y.
component,
and suppresses low frequency components in the output Y.
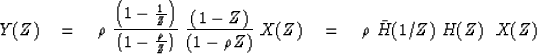
![]() because the filter coefficients are not complex numbers.
H(Z) is called a causal filter because it uses past values
of the filter inputs to create the output.
Likewise H(1/Z) is called anticausal because the present output
comes from future inputs.
If you filter with both,
because the filter coefficients are not complex numbers.
H(Z) is called a causal filter because it uses past values
of the filter inputs to create the output.
Likewise H(1/Z) is called anticausal because the present output
comes from future inputs.
If you filter with both,
![]() ,the filter response is
,the filter response is
![]() (to the extent that a time derivate is the same as a finite difference).
(to the extent that a time derivate is the same as a finite difference).
![]() whose
amplitude response is
whose
amplitude response is ![]() ,or the causal filter H(Z) whose
energy response is
,or the causal filter H(Z) whose
energy response is ![]() .The causal filter
.The causal filter