|
|
|
|
Modeling ocean-bottom seismic rotation rates |
The elastic isotropic wave equation has two state variables: the stress tensor and the particle velocity vector. The particle velocities are propagated by:
where
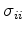 are the normal stresses,
are the normal stresses,
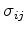 are the transverse stresses,
are the transverse stresses, 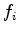 is a particle velocity force function in direction
is a particle velocity force function in direction 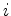 ,
, 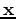 is the spatial source location operating at time
is the spatial source location operating at time 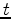 ,
, 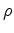 is density and
is density and 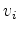 is the particle velocity in direction
is the particle velocity in direction 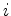 . The stresses are propagated using the stress-displacement relation:
. The stresses are propagated using the stress-displacement relation:
where 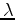 and
and 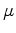 are the Lam
are the Lam
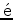 elastic constants and
elastic constants and 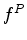 is a pressure force function. The pressure force is added equally to the normal stresses to generate a P-wave source.
is a pressure force function. The pressure force is added equally to the normal stresses to generate a P-wave source.
We use the staggered time grid methodology for elastic propagation (Virieux, 1986), in which the stresses and particle velocities are half a time step apart. Therefore equations 1 and 2 are solved in alternation during the propagation.
The divergence of particle displacements is proportional to the pressure in the medium, the proportion being the medium parameters. It is equal to the average of the normal stresses in the stress tensor:
where 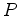 is the pressure value and
is the pressure value and
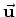 are the displacements. Pressure waves cause a volumetric deformation in the medium, and their value can therefore be extracted by using equation 3 on forward modeled wavefields. However, other wave types can also generate a volumetric deformation at free surfaces, as a result of the discontinuity of the stresses.
are the displacements. Pressure waves cause a volumetric deformation in the medium, and their value can therefore be extracted by using equation 3 on forward modeled wavefields. However, other wave types can also generate a volumetric deformation at free surfaces, as a result of the discontinuity of the stresses.
We define rotation as the first time derivative of the curl of displacements:
The curl operation results in the non-volumetric part of the deformation, i.e. the ``shear'' deformation. At a free surface, this deformation will cause a rotation. In an isotropic medium, the curl is associated with S-waves. However, at a free surface, both P-waves and surface waves will also generate non-volumetric deformation. The units we use for rotations in this paper are
milliradians
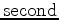 .
.
|
|
|
|
Modeling ocean-bottom seismic rotation rates |