|
|
|
|
Computational analysis of extended full waveform inversion |
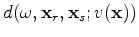 is the modeled data,
is the modeled data,
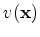 is the velocity model,
is the velocity model,
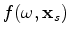 is the source function,
is the source function, 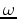 is frequency,
is frequency,
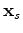 and
and
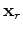 are the source and receiver coordinates, and
are the source and receiver coordinates, and 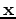 is the model coordinate. In the acoustic, constant-density case, the Green's function
is the model coordinate. In the acoustic, constant-density case, the Green's function
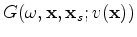 satisfies:
satisfies:
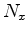 ,
, 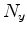 and
and 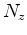 , are the number of points along the three spatial axes,
, are the number of points along the three spatial axes,
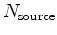 is the number of sources,
is the number of sources,
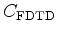 is the cost of convolving one model location by the time-domain finite-difference stencil and
is the cost of convolving one model location by the time-domain finite-difference stencil and 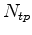 is the number of time samples for propagation. By linearizing equation 1 over the squared slowness, we can compute the adjoint as:
is the number of time samples for propagation. By linearizing equation 1 over the squared slowness, we can compute the adjoint as:
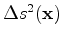 is the perturbation in squared slowness and
is the perturbation in squared slowness and 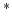 denotes the complex conjugate. For the adjoint, the imaging time sampling can be much larger than that of propagation since it does not need to satisfy the dispersion and stability conditions. Hence, the cost of computing the adjoint of FWI can be written as:
denotes the complex conjugate. For the adjoint, the imaging time sampling can be much larger than that of propagation since it does not need to satisfy the dispersion and stability conditions. Hence, the cost of computing the adjoint of FWI can be written as:
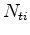 is the number of time samples for imaging. The total cost of one iteration of FWI becomes
is the number of time samples for imaging. The total cost of one iteration of FWI becomes
|
|
|
|
Computational analysis of extended full waveform inversion |