|
|
|
|
Decon in the log domain with variable gain |
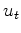 in the log spectrum of the deconvolution filter.
Given data
in the log spectrum of the deconvolution filter.
Given data 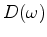 , the deconvolved output is
, the deconvolved output is
![$\displaystyle r_t \ =\ {\rm FT}^{-1}\ \left[ D(\omega)\ \exp\left( \sum_t u_tZ^t \right) \right]$](img6.png) |
(1) |
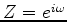 .
The log variables
.
The log variables 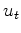 transform the linear least squares (
transform the linear least squares (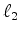 ) problem
to a non-linear one that requires iteration.
Losing the linearity is potentially a big loss,
but we lost that at the outset when we first realized
we needed to deal with the non-minimum phase Ricker wavelet.
We find convergence is typically quite rapid.
) problem
to a non-linear one that requires iteration.
Losing the linearity is potentially a big loss,
but we lost that at the outset when we first realized
we needed to deal with the non-minimum phase Ricker wavelet.
We find convergence is typically quite rapid.
The source wavelet, inverse to the decon filter above, corresponds to 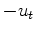 .
The positive lag coefficients in
.
The positive lag coefficients in 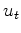 correspond
to a causal minimum phase wavelet.
The negative lag coefficients correspond to an anticausal filter.
correspond
to a causal minimum phase wavelet.
The negative lag coefficients correspond to an anticausal filter.
Here for the first time we introduce the complication
that seismic data is non-stationary
requiring a time variable gain 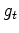 .
The deconvolved data is the residual
.
The deconvolved data is the residual 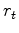 .
The gained residual
.
The gained residual
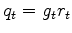 is ``sparsified''
(Li et al., 2012)
by minimizing
is ``sparsified''
(Li et al., 2012)
by minimizing
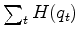 where
where
Our prefered penalty function 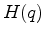 used for finding
used for finding 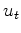 is the hyperbolic (or hybrid) penalty function
(equation (3)).
The output
is the hyperbolic (or hybrid) penalty function
(equation (3)).
The output 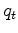 best senses sparsity when
gain is such that the typical penalty
best senses sparsity when
gain is such that the typical penalty 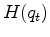 value
is found near the transition level between
value
is found near the transition level between 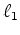 and
and 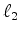 norms,
namely, when typical
norms,
namely, when typical
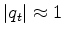 .
.
|
|
|
|
Decon in the log domain with variable gain |