Two-parameters residual-moveout analysis for wave-equation migration velocity analysis

Two-parameter RMO functions

Biondi and Symes (2004) introduced the following one-parameter RMO function for angle-domain CIG:

$$\Delta z = \left(1-\rho\right) \tan^2 \gamma,$$ (1)

where $\gamma$ is the aperture angle and $\Delta z$ is the difference between the imaged depth at normal incidence ($\gamma=0$ ) and the imaged depth at a given angle $\gamma$ . For constant velocity errors in the half space above the reflector, the parameter $\rho$ has a direct physical interpretation. It is related to the ratio between the current migration slowness $s_{\rm mig}$ and the true slowness $s$ ; that is, $\rho \approx s_{\rm mig}/s$ . However, in the following discussion this physical interpretation of $\rho$ is irrelevant, and it can be simply considered as a free parameter describing a family of RMO functions.

What I call the Taylor RMO function adds the next higher-order even term to equation 1 as follows

$${\Delta z}_T = \left(1-\rho\right) \tan^2 \gamma + \left(1-\lambda_T\right) \tan^4 \gamma,$$ (2)

where $\lambda_T$ is the additional free parameter. As in equation 1, the RMO function is equally flat when $\rho=1$ and $\lambda_T=1$ .

The second two-parameter RMO function that I introduce adds a sine function to equation 1 as follows

$${\Delta z}_O = \left(1-\rho\right) \tan^2 \gamma + \left(1-\lambda_O\right) \vert\sin \bar{\gamma}\vert,$$ (3)

where $\lambda_O$ is the additional free parameter, $\bar{\gamma}=2\pi\gamma/\gamma_{\rm max}$ is the normalized aperture angle, and $\gamma_{\rm max}$ is the maximum aperture angle used for the analysis.

Cig
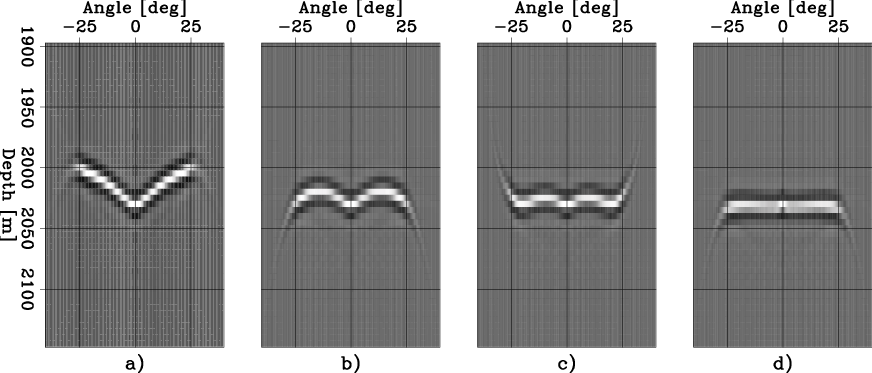
Figure 1. CIGs after constant velocity migration and: a) no correction, b) correction with a one-parameter RMO (equation 1), c) correction with the ``Taylor'' RMO (equation 2), and d) correction with the ``Orthogonal'' RMO (equation 3).

Figure 1a shows the first CIG that I use for my study. It was obtained by migrating a synthetic data set that was modeled assuming a strong negative velocity anomaly above a flat reflector and migrated assuming a constant velocity (Biondi, 2011). This CIG is located under the center of the anomaly. Its moveout is not well described by the conventional RMO function expressed in equation 1 because the image at near angles is more affected by the anomaly than the image at far angles. Figure 1b shows the result of correcting this CIG using equation 1 with $\rho=1.075$ that is the $\rho$ value corresponding to the maximum of the stack power picked from a stack-power spectrum. This corrected CIG is far from being flat.

Smooth
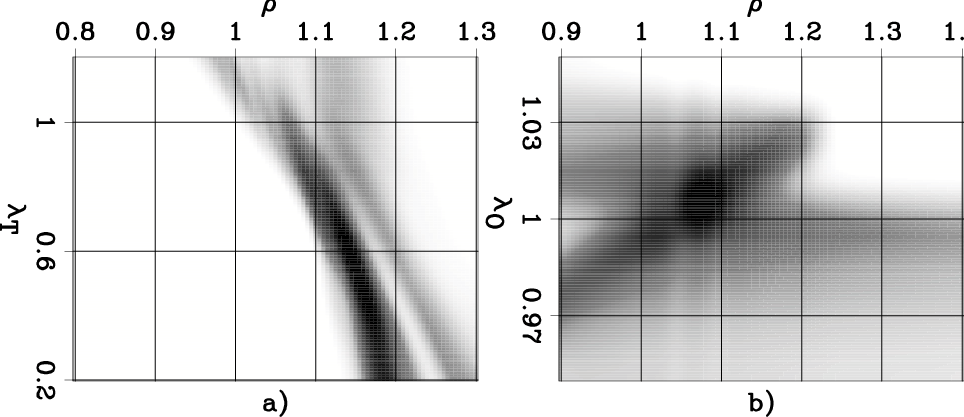
Figure 2. Two-parameter stack-power spectra resulting from RMO analysis of the migrated CIG shown in Figure 1a obtained applying: a) the ``Taylor'' RMO function (equation 2), and b) the ``Orthogonal'' RMO function (equation 3).

Figure 2 shows stack-power spectra as a function of two parameters. The panel on the left (Figure 2a) was computed using the ``Taylor'' RMO function described by equation 2, whereas the panel on the right (Figure 2b) was computed using the ``Orthogonal'' RMO function described by equation 3. In both cases the stack power was computed over the range of $-25^o \leq \gamma \leq 25^o$ . Consequently, I set $\gamma_{\rm max}=25^o$ to compute the normalized angle $\bar{\gamma}$ in equation 3. The power spectra were averaged over a thick (200 m) depth interval and slightly smoothed along the RMO parameters $\rho$ and $\lambda$ .

The maxima of both of these two-parameter spectra are not along the $\lambda=1$ line, indicating that the two-parameter RMO improves the flatness with respect to the one-parameter RMO. Indeed, when the values corresponding to the maxima of the power spectra shown in Figure 2 are used to correct the original CIG I obtain flatter gathers than when using a one-parameter RMO. Figure 1c shows the result of correcting the CIG shown Figure 1a using equation 2 with $\rho=1.15$ and $\lambda_T=.55$ . Figure 1c shows the result of correcting the CIG shown Figure 1a using equation 3 with $\rho=1.075$ and $\lambda_O=1.0055$ . The CIG corrected using the ``Orthogonal'' RMO is almost perfectly flat within the $-25^o \leq \gamma \leq 25^o$ range.

Notice that the shape of the spectra around their respective maxima is substantially different between the two plots. The function corresponding to the ``Orthogonal'' RMO is more isotropic around the maximum than the one corresponding to the ``Taylor'' RMO. This behavior is expected because the two terms of the ``Orthogonal'' RMO function are close to be orthogonal with respect to each other. Theoretically, this more isotropic shape could lead to better gradients. However, we can also notice diagonal artifacts in Figure 2b. As we discuss below, the effects of these artifacts tend to outweigh any advantage provided by the more isotropic shape of the spectrum.

Cig-aniso
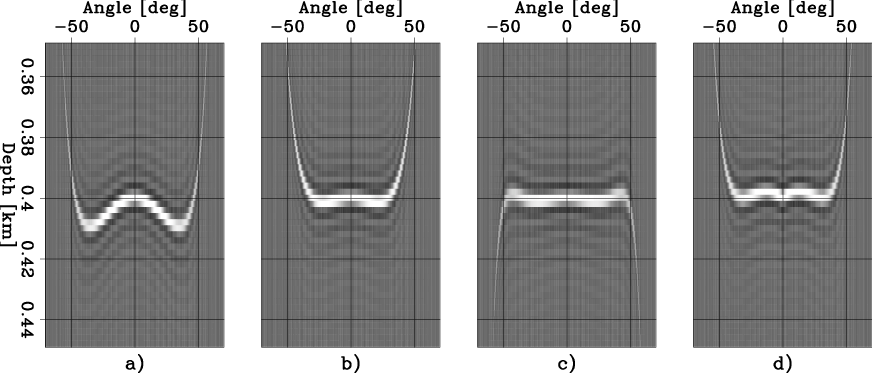
Figure 3. CIGs after isotropic velocity migration and: a) no correction, b) correction with a one-parameter RMO (equation 1), c) correction with the ``Taylor'' RMO (equation 2), and d) correction with the ``Orthogonal'' RMO shows the second CIG that I use (equation 3).

Figure 3a shows the second CIG that I use for my analysis. It was obtained by migrating a synthetic data set that was modeled assuming a strongly anisotropic VTI medium ( $\epsilon=0.0975$ and $\delta=-0.11$ ) above a flat reflector, and migrated assuming an isotropic velocity (Biondi, 2005). Because the anisotropy in the medium is not taken into account by the isotropic migration, the CIG moveout is not well described by the conventional one-parameter RMO function expressed in equation 1. Figure 1b shows the result of correcting this CIG using equation 1 with $\rho=.9375$ that is the $\rho$ value corresponding to the maximum of the stack power picked from a stack-power spectrum. This corrected CIG is far from being flat.

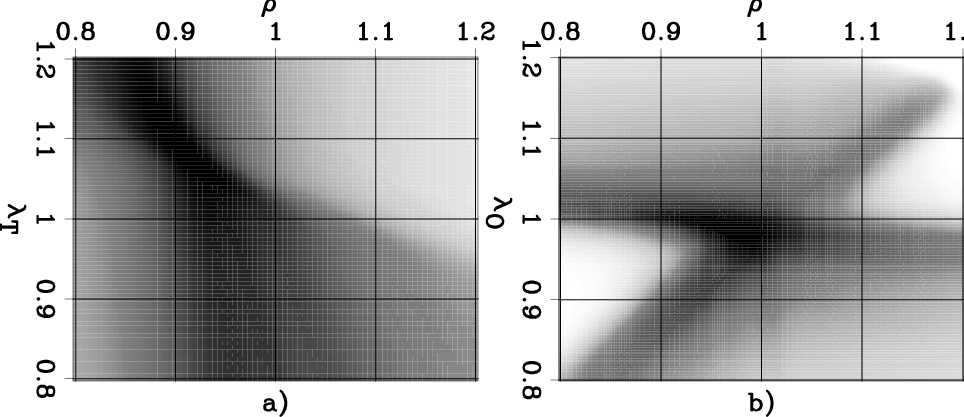
Figure 4 shows stack-power spectra as a function of two parameters. The panel on the left (Figure 4a) was computed using the ``Taylor'' RMO function described by equation 2, whereas the panel on the right (Figure 4b) was computed using the ``Orthogonal'' RMO function described by equation 3. In both cases the stack power was computed over the range of $-50^o \leq \gamma \leq 50^o$ . Consequently, I set $\gamma_{\rm max}=50^o$ to compute the normalized angle $\bar{\gamma}$ in equation 3. The power spectra were averaged over a thick (200 m) depth interval and slightly smoothed along the RMO parameters $\rho$ and $\lambda$ .

Smooth-aniso
Figure 4. Two-parameter stack-power spectra resulting from RMO analysis of the migrated CIG shown in Figure 3a obtained applying: a) the ``Taylor'' RMO function (equation 2), and b) the ``Orthogonal'' RMO function (equation 3).

As for the spectra computed from the first CIG (Figure 2), the function corresponding to the ``Orthogonal'' RMO is more isotropic around the maximum than the one corresponding to the ``Taylor'' RMO. This difference in shape is less pronounced for this example than for the previous one.

Because the maxima of both of these two-parameter spectra are not along the $\lambda=1$ line, we have indication that the two-parameter RMO improves the flatness with respect to the one-parameter RMO. Indeed, when the values corresponding to the maxima of the power spectra shown in Figure 4 are used to correct the original CIG I obtain flatter gathers than when using a one-parameter RMO. Figure 3c shows the result of correcting the CIG shown Figure 3a using equation 2 with $\rho=0.915$ and $\lambda_T=1.075$ . Figure 3c shows the result of correcting the CIG shown Figure 3a using equation 3 with $\rho=0.97$ and $\lambda_O=0.988$ . In particular, the CIG corrected using the ``Taylor'' RMO is significantly flatter, within the $-50^o \leq \gamma \leq 50^o$ range, than the one corrected using a one-parameter RMO.

Two-parameters residual-moveout analysis for wave-equation migration velocity analysis