Pseudoinverse estimate

From (iterationons), it follows easily that the model estimate at the n-th iteration must be of the form

s_n = _i=1^n-1 _i+1p_i,   where we assume for simplicity that ${\bf s}_1 = 0$.Then substituting (optimumalpha) -- or more directly the first ratio in (cgalpha) -- for the $\alpha_i$'s shows that the n-th iterate is given explicitly by

s_n = _j=1^n-1 p_jp_j^T (p_j,M^TMp_j)g_j = _j=1^n-1 p_jp_j^T (p_j,M^TMp_j)M^Tt   for this scheme. The resulting approximate inverse operator is therefore

(M^TM)^ _j=1^n-1 p_jp_j^T (p_j,M^TMp_j),   which form we now want to study. We use the dagger notation to indicate that the expression in (inversionop) is approximating a pseudoinverse, because it may happen that the normal matrix is singular in which case the standard inverse does not exist.

First, note that although (inversionop) might appear to be in the form of a singular value decomposition, it definitely is not. The ${\bf p}_n$'s are not orthogonal and the denominators of these terms are not eigenvalues. If we define the matrix composed of direction vectors at the n-th iteration to be

P_n = (

),   then the approximate inverse operator can be rewritten as

(M^TM)^ P_nD_P^-1P_n^T,   where the matrix ${\bf D_P}$ is a diagonal matrix whose diagonal elements are given by $D_{jj} = ({\bf p}_j,{\bf M}^T{\bf Mp}_j)$.In fact the entire matrix is given directly by

D_P P_n^TM^TMP_n,   because of the conjugacy of the ${\bf p}$'s composing ${\bf P}_n$.Now equation (pn) shows that

P_nB_n = G_n,   where

G_n = (

),   and the matrix ${\bf B}_n$ is bidiagonal with units along the main diagonal and $\beta$'s along the upper diagonal:

B_n = [

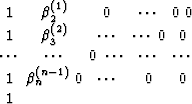
]   Multiplying (PBG) on the right by the inverse of ${\bf B}_n$ and then substituting into (inverse2), we find that

(M^TM)^ G_nB_n^-1D_P^-1(B_n^T)^-1G_n^T.   Thus, the approximate inverse is seen to have the general form

(M^TM)^ G_nT_n^-1G_n^T,   where ${\bf T}_n$ is the tridiagonal matrix

T_n = B_n^TD_PB_n.   This result highlights the similarities between the CG method and that of other iterative methods such as Lanczos 1950 and LSQR Paige and Saunders (1982), also producing tridiagonal respresentations of the matrix to be inverted.