




Next: MORE ON GAUSSIAN CURVATURE
Up: Claerbout & Fomel: Gaussian
Previous: What is the L1
I proposed that we find out the differential equation
that describes the bending of paper
and use it as a regularization.
The idea is to encourage a Busch-like behavior.
As with L1, I would like to have a linear operator to preserve
the uniqueness of the solution. Uniqueness gives reliability.
My exerience has taught me that if a method has multiple isolated minima,
I will descend into the wrong one.
If the paper-bending operator is nonlinear, I could linearize it.
Bill Symes suggested the Gaussian curvature.
My favorite search engine (google.com) quickly gave me several references.
Indeed a sheet of paper does seem to have a Gaussian curvature of zero.
The Gaussian curvature of a 2-D function vanishes
wherever the the function is locally one dimensional.
The Gaussian curvature is the product of the principal curvatures.
The Gaussian curvature is
| 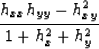 |
(10) |
For small dips, the numerator is the important part.
The numerator is the determinant of the Hessian,
| 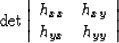 |
(11) |
We might regularize a collection of data points
by minimizing this determinant.
I have begun looking for references that may have previously
investigated this very basic idea.
Unfortunately, the function is nonlinear.
We can linearize it.
Replacing h by 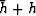 and dropping terms in h2 we get
and dropping terms in h2 we get
| 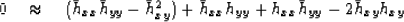 |
(12) |
The most important question is: what is 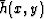 ?
How do we initialize it, and how can we safely update it?
A way to initialize
?
How do we initialize it, and how can we safely update it?
A way to initialize 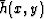 is to approximate the initial data
by a best fitting one-dimensional parabola.
One way to stablize
is to approximate the initial data
by a best fitting one-dimensional parabola.
One way to stablize 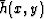 is to smooth it in patches.
is to smooth it in patches.
I am reminded of "LOMOPLAN", an earlier idea I had to fit a best
plane wave,
then use it to define a linear operator to use
as a weighting function in estimation.
The idea is that a sedimentary section consists of a single local plane wave.
Perhaps that two-stage least squares process is akin to
linearizing the Gaussian curvature.





Next: MORE ON GAUSSIAN CURVATURE
Up: Claerbout & Fomel: Gaussian
Previous: What is the L1
Stanford Exploration Project
5/1/2000
![]() and dropping terms in h2 we get
and dropping terms in h2 we get