




Next: About this document ...
Up: Downward continuation of waves
Previous: Linking Snell waves to
By now you are probably wondering what good are downward-continued
seismic waves.
The answer is that once we know the wavefields inside the earth
we can do many seismic data analysis tasks.
The obvious one is migration.
We can do it better than Kirchhoff.
Given the upcoming wave at the earth surface 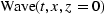 , pushing
it down to all z in the earth gives us
, pushing
it down to all z in the earth gives us 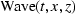 .The exploding reflector idea is that the source
is on the reflectors at t=0.
Thus we construct images with
.The exploding reflector idea is that the source
is on the reflectors at t=0.
Thus we construct images with
|  |
(21) |
There is a curious symmetry between the input and output
of the imaging process:
|
|
| t = 0 |
|
|
| |
|
|
all |
|
|
| |
|
|
| |
|
|
Diffraction
is sometimes regarded as the natural process that creates
and enlarges hyperboloids.
Migration
is the computer process that does the reverse.
Compared to the Kirchhoff method,
downward continuation methods offer several advantages:
(1) we handle v(z) media exactly without calculating any ray paths;
(2) we get the correct amplitude versus angle;
(3) we automatically include various phase shifts and wave phenomena;
(4) interpolation and aliasing artifacts are much reduced.





Next: About this document ...
Up: Downward continuation of waves
Previous: Linking Snell waves to
Stanford Exploration Project
3/1/2001