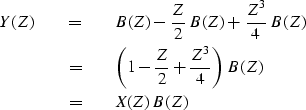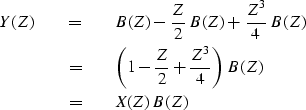Next: Convolution equation and program
Up: SAMPLED DATA AND Z-TRANSFORMS
Previous: Linear superposition
Now suppose there was an explosion at t = 0,
a half-strength implosion at t = 1,
and another, quarter-strength explosion at t = 3.
This sequence of events determines a ``source'' time series,
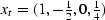 .The Z-transform of the source is
.The Z-transform of the source is
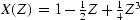 .The observed yt for this sequence of explosions and implosions
through the seismometer has a Z-transform Y(Z), given by
.The observed yt for this sequence of explosions and implosions
through the seismometer has a Z-transform Y(Z), given by
| 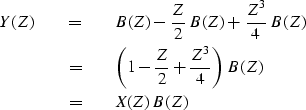 |
|
| |
| (4) |
The last equation
shows polynomial multiplication as the
underlying basis of time-invariant linear-system theory,
namely that the output Y(Z) can be expressed as the input X(Z) times
the impulse-response filter B(Z).
When signal values are insignificant
except in a ``small'' region on the time axis,
the signals are called ``wavelets.''





Next: Convolution equation and program
Up: SAMPLED DATA AND Z-TRANSFORMS
Previous: Linear superposition
Stanford Exploration Project
3/1/2001