




Next: About this document ...
Up: CORRELATION AND SPECTRA
Previous: Common signals
Filters
are often used to change the spectra of given data.
With input X(Z),
filters B(Z), and output Y(Z), we have
Y(Z) = B(Z)X(Z) and the Fourier conjugate
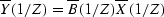 .
Multiplying these two relations together, we get
which says that the spectrum of the input times the spectrum
of the filter equals the spectrum of the output.
Filters are often characterized by the shape of their spectra;
this shape is the same as the
spectral ratio
of the output over the input:
.
Multiplying these two relations together, we get
which says that the spectrum of the input times the spectrum
of the filter equals the spectrum of the output.
Filters are often characterized by the shape of their spectra;
this shape is the same as the
spectral ratio
of the output over the input:
| 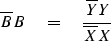 |
(49) |
EXERCISES:
-
Suppose a wavelet is made up of complex numbers.
Is the autocorrelation relation sk = s-k true?
Is sk real or complex? Is
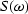 real or complex?
real or complex?





Next: About this document ...
Up: CORRELATION AND SPECTRA
Previous: Common signals
Stanford Exploration Project
3/1/2001