|
data
Figure 5 The input data are irregularly sampled. | 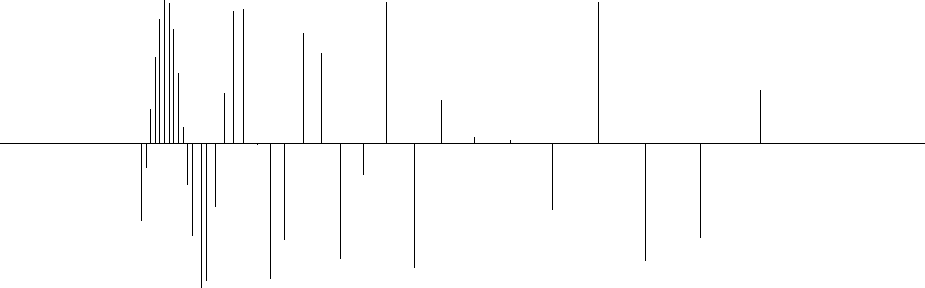 |
|
data
Figure 5 The input data are irregularly sampled. |  |
The first example is a simple synthetic test for 1-D inverse
interpolation. The input data were randomly subsampled (with
decreasing density) from a sinusoid (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The
forward operator
). The
forward operator ![]() in this case is linear interpolation. We seek
a regularly sampled model that could predict the data with a
forward linear interpolation. Sparse irregular distribution of the
input data makes the regularization enforcement a necessity.
I applied convolution with the simple (1,-1)
difference filter as the operator
in this case is linear interpolation. We seek
a regularly sampled model that could predict the data with a
forward linear interpolation. Sparse irregular distribution of the
input data makes the regularization enforcement a necessity.
I applied convolution with the simple (1,-1)
difference filter as the operator ![]() that forces model continuity
(the first-order spline).
An appropriate preconditioner
that forces model continuity
(the first-order spline).
An appropriate preconditioner ![]() in this
case is recursive causal integration.
in this
case is recursive causal integration.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
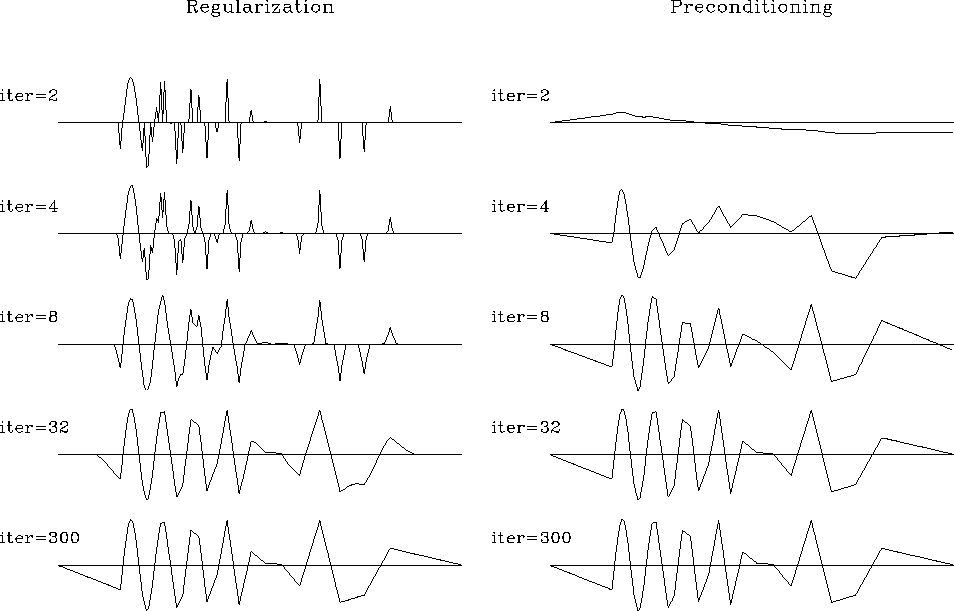
As expected,
preconditioning provides a much faster rate of convergence.
Since iteration to the exact solution
is never achieved in large-scale problems,
the results of iterative optimization may turn out quite differently.
Bill Harlan points out that the two goals
in (8) conflict with each other:
the first one enforces ``details'' in the model,
while the second one tries to smooth them out.
Typically, regularized optimization creates
a complicated model at early iterations.
At first, the data fitting goal (8) plays a more important role.
Later, the regularization goal (8) comes into play
and simplifies (smooths) the model as much as needed.
Preconditioning acts differently.
The very first iterations create a simplified (smooth) model.
Later, the data fitting goal adds more details into the model.
If we stop the iterative process early,
we end up with an insufficiently complex model,
not in an insufficiently simplified one.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) provides a clear illustration of Harlan's observation.
provides a clear illustration of Harlan's observation.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) measures the rate of convergence by the model residual,
which is a distance from the current model to the final solution.
It shows that preconditioning saves many iterations.
Since the cost of each iteration for each method is roughly equal,
the efficiency of preconditioning is evident.
measures the rate of convergence by the model residual,
which is a distance from the current model to the final solution.
It shows that preconditioning saves many iterations.
Since the cost of each iteration for each method is roughly equal,
the efficiency of preconditioning is evident.
|
schwab1
Figure 7 Convergence of the iterative optimization, measured in terms of the model residual. The ``p'' points stand for preconditioning; the ``r'' points, regularization. | 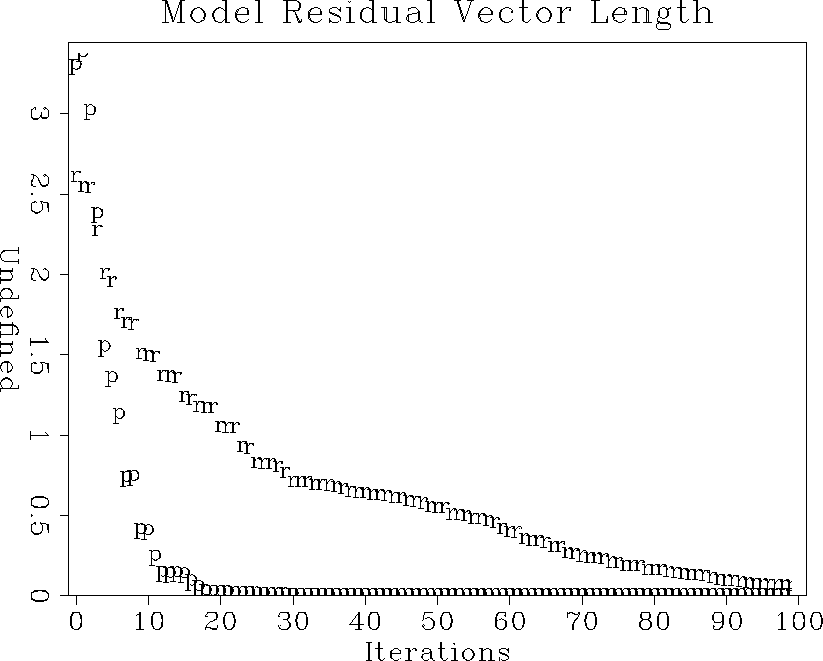 |
The module invint2 ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) invokes the solvers to make
Figures
invokes the solvers to make
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
We use convolution with
helicon
.
We use convolution with
helicon ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) for the regularization
and we use deconvolution with
polydiv
for the regularization
and we use deconvolution with
polydiv ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) for the preconditioning.
The code looks fairly straightforward except for
the oxymoron
known=aa%mis.
invint2Inverse linear interpolation
for the preconditioning.
The code looks fairly straightforward except for
the oxymoron
known=aa%mis.
invint2Inverse linear interpolation