




Next: Wilson-Burg theory
Up: The helical coordinate
Previous: Kolmogoroff spectral factorization
(If you are new to this material, you should pass over this section.)
Spectral factorization is the job of taking a power spectrum
and from it finding a causal (zero before zero time) filter with that spectrum.
Methods for this task (there are many)
not only produce a causal wavelet,
but they typically produce one whose
convolutional inverse is also causal.
(This is called the ``minimum phase'' property.)
In other words, with such a filter we can do stable deconvolution.
Here
I introduce a new method of spectral factorization
that looks particularly suitable for the task at hand.
I learned this new method from John Parker Burg who
attributes it to an old paper by Wilson
(I find Burg's explanation, below, much clearer than Wilson's.)
Below find subroutine lapfac() which
was used in the previous section
to factor the Laplacian operator.
To invoke the factorization subroutine,
you need to supply one side of an autocorrelation function.
For example, let us specify the negative of the 2-D Laplacian
(an autocorrelation)
in a vector n = 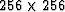 points long.
points long.
rr(1) = 4.
rr(2) = -1.
rr(1+256) = -1.
Subroutine lapfac()
finds the helical derivative (factored negative Laplacian)
and then prepares the required filter
coefficient tables for the helix convolution
and deconvolution subroutines.
lapfacfactor 2-D Laplacian
Subroutine lapfacn() has its main job
done by subroutine wilson_factor() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shown after the Wilson-Burg theory.
shown after the Wilson-Burg theory.
![]() points long.
points long.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shown after the Wilson-Burg theory.
shown after the Wilson-Burg theory.