The Rocca operator ![]() says to spray out an ellipse and then sum over a circle.
This approach,
associated with Gerry Gardner,
says that we are interested in all circles
that are inside and tangent to an ellipse,
since only the ones that are tangent
will have a constructive interference.
says to spray out an ellipse and then sum over a circle.
This approach,
associated with Gerry Gardner,
says that we are interested in all circles
that are inside and tangent to an ellipse,
since only the ones that are tangent
will have a constructive interference.
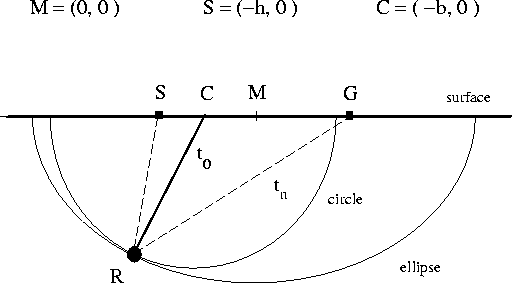
The Gardner formulation answers this question: Given a single nonzero offset impulse, which events on the zero-offset section will result in the same migrated subsurface picture? Since we know the migration response of a zero and nonzero offset impulses (circle and ellipse) we can rephrase this question: Given an ellipse corresponding to a nonzero offset impulse, what are the circles tangent to it that have their centers at the earth's surface? These circles if superposed will yield the ellipse. Furthermore, each of these circles corresponds to an impulse on the zero-offset section. The set of these impulses in the zero offset section is the DMO+NMO impulse response for a given nonzero offset event.
 |