MINIMUM-PHASE FILTERS

Let b_t denote a filter. Then a_t is its inverse filter if the convolution of a_t with b_t is an impulse function. In terms of Z-transforms, an inverse is simply defined by A(Z) = 1/B(Z). Whether the filter A(Z) is causal depends on whether it is finite everywhere inside the unit circle, or really on whether B(Z) vanishes anywhere inside the circle. For example, B(Z)=1-2Z vanishes at Z = 1/2. There A(Z)=1/B(Z) must be infinite, that is to say, the series A(Z) must be nonconvergent at Z = 1/2. Thus, as we have just seen, a_t is noncausal. A most interesting case, called ``minimum phase," occurs when both a filter B(Z) and its inverse are causal. In summary,

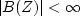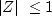		causal: 		 $\vert B(Z)\vert < \infty$ for $\vert Z\vert \ \le 1$		causal inverse: 	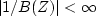	 $\vert 1/B(Z)\vert < \infty$ for $\vert Z\vert \ \le 1$ 
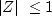		minimum phase: 		 both above conditions

The reason the interesting words ``minimum phase'' are used is given in chapter .