




Next: NONSTATIONARITY
Up: HOW TO DIVIDE NOISY
Previous: Explicit model for noise
Equation (24) and its surrounding theory
are easily misunderstood and misused.
I would like to show you a pitfall.
Equation (24) expresses the answer
to the deconvolution problem,
but does so in terms of the unknowns
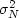 and
and
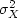 .Given an initial estimate
of
.Given an initial estimate
of 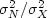 ,we see that
equation (24) gives us X and
(19) gives N,
so that we can compute
,we see that
equation (24) gives us X and
(19) gives N,
so that we can compute
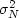 and
and
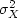 .Presumably these computed values are better than our initial guesses.
In statistics,
the variances in equation (24)
are called ``priors,"
and it makes sense to check them,
and even more sense to correct them.
From the corrected values we should be able to iterate,
further improving the corrections.
Equation (24) applies for each of the many frequencies,
and there is only a single unknown,
the ratio
.Presumably these computed values are better than our initial guesses.
In statistics,
the variances in equation (24)
are called ``priors,"
and it makes sense to check them,
and even more sense to correct them.
From the corrected values we should be able to iterate,
further improving the corrections.
Equation (24) applies for each of the many frequencies,
and there is only a single unknown,
the ratio 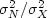 .Hence it seems as if we have plenty of information,
and the bootstrapping procedure might work.
A pessimist might call this bootstrapping
a self-fulfilling prophecy, but we will see.
What do you think?
.Hence it seems as if we have plenty of information,
and the bootstrapping procedure might work.
A pessimist might call this bootstrapping
a self-fulfilling prophecy, but we will see.
What do you think?
Truth is stranger than fiction.
I tried bootstrapping the variances.
With my first starting value for
the ratio 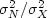 ,iterating led to the ratio being infinite.
Another starting value led to the ratio being zero.
All starting values led to zero or infinity.
Eventually I deduced that there must be a metastable starting value.
Perhaps the metastable value is the appropriate one,
but I lack a rationale to assert it.
It seems we cannot bootstrap the variances
because the solutions produced do not tend to the correct variance,
nor is the variance ratio correct.
Philosophically, we can be thankful
that these results failed to converge,
since this outcome prevents us
from placing a false confidence in the bootstrapping procedure.
,iterating led to the ratio being infinite.
Another starting value led to the ratio being zero.
All starting values led to zero or infinity.
Eventually I deduced that there must be a metastable starting value.
Perhaps the metastable value is the appropriate one,
but I lack a rationale to assert it.
It seems we cannot bootstrap the variances
because the solutions produced do not tend to the correct variance,
nor is the variance ratio correct.
Philosophically, we can be thankful
that these results failed to converge,
since this outcome prevents us
from placing a false confidence in the bootstrapping procedure.
|
The variance of the solution to a least-squares problem
is not usable to bootstrap to a better solution.
|
I conclude that linear-estimation theory,
while it appears
to be a universal guide to practice,
is actually incomplete.
Its incompleteness grows even more significant in later chapters,
when we apply least squares to multivariate problems where
the scalar 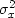 becomes a matrix.
We continue our search for ``universal truth'' by studying more examples.
becomes a matrix.
We continue our search for ``universal truth'' by studying more examples.
EXERCISES:
-
Using the chain rule for differentiation,
verify that
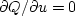 and
and 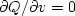 is equivalent to
is equivalent to 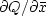 , where x=u+iv.
, where x=u+iv.
-
Write code to verify
the instability in estimating the variance ratio.
1
1





Next: NONSTATIONARITY
Up: HOW TO DIVIDE NOISY
Previous: Explicit model for noise
Stanford Exploration Project
10/21/1998
![]() ,iterating led to the ratio being infinite.
Another starting value led to the ratio being zero.
All starting values led to zero or infinity.
Eventually I deduced that there must be a metastable starting value.
Perhaps the metastable value is the appropriate one,
but I lack a rationale to assert it.
It seems we cannot bootstrap the variances
because the solutions produced do not tend to the correct variance,
nor is the variance ratio correct.
Philosophically, we can be thankful
that these results failed to converge,
since this outcome prevents us
from placing a false confidence in the bootstrapping procedure.
,iterating led to the ratio being infinite.
Another starting value led to the ratio being zero.
All starting values led to zero or infinity.
Eventually I deduced that there must be a metastable starting value.
Perhaps the metastable value is the appropriate one,
but I lack a rationale to assert it.
It seems we cannot bootstrap the variances
because the solutions produced do not tend to the correct variance,
nor is the variance ratio correct.
Philosophically, we can be thankful
that these results failed to converge,
since this outcome prevents us
from placing a false confidence in the bootstrapping procedure.
![]() becomes a matrix.
We continue our search for ``universal truth'' by studying more examples.
becomes a matrix.
We continue our search for ``universal truth'' by studying more examples.