




Next: Conjugate gradient
Up: ITERATIVE METHODS
Previous: Conditioning the gradient
Before we can understand why the conjugate-gradient method is so fast,
we need to see why the
steepest-descent method
is so slow.
The process of selecting  is called ``line search,"
but for a linear problem like the one we have chosen here,
we hardly recognize choosing
is called ``line search,"
but for a linear problem like the one we have chosen here,
we hardly recognize choosing  as searching a line.
A more graphic understanding of the whole process is possible
in a two-dimensional space where the vector of unknowns x
has just two components, x1 and x2.
Then the size of the residual vector
as searching a line.
A more graphic understanding of the whole process is possible
in a two-dimensional space where the vector of unknowns x
has just two components, x1 and x2.
Then the size of the residual vector 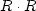 can be
displayed with a contour plot in the plane of (x1,x2).
Visualize a contour map of a mountainous terrain.
The gradient is perpendicular to the contours.
Contours and gradients are curved lines.
In the steepest-descent method we start at a point
and compute the gradient direction at that point.
Then we begin a straight-line descent in that direction.
The gradient direction curves away from our direction of travel,
but we continue on our straight line
until we have stopped descending and are about to ascend.
There we stop, compute another gradient vector,
turn in that direction, and descend along a new straight line.
The process repeats until we get to the bottom,
or until we get tired.
can be
displayed with a contour plot in the plane of (x1,x2).
Visualize a contour map of a mountainous terrain.
The gradient is perpendicular to the contours.
Contours and gradients are curved lines.
In the steepest-descent method we start at a point
and compute the gradient direction at that point.
Then we begin a straight-line descent in that direction.
The gradient direction curves away from our direction of travel,
but we continue on our straight line
until we have stopped descending and are about to ascend.
There we stop, compute another gradient vector,
turn in that direction, and descend along a new straight line.
The process repeats until we get to the bottom,
or until we get tired.
What could be wrong with such a direct strategy?
The difficulty is at the stopping locations.
These occur where the descent direction
becomes parallel to the contour lines.
(There the path becomes horizontal.)
So after each stop, we turn 90 ,from parallel to perpendicular to the local contour line
for the next descent.
What if the final goal is at a 45
,from parallel to perpendicular to the local contour line
for the next descent.
What if the final goal is at a 45 angle to our path?
A 45
angle to our path?
A 45 turn cannot be made.
Instead of moving like a rain drop down the centerline of a rain gutter,
we move along a fine-toothed zigzag path,
crossing and recrossing the centerline.
The gentler the slope of the rain gutter,
the finer the teeth on the zigzag path.
1
turn cannot be made.
Instead of moving like a rain drop down the centerline of a rain gutter,
we move along a fine-toothed zigzag path,
crossing and recrossing the centerline.
The gentler the slope of the rain gutter,
the finer the teeth on the zigzag path.
1





Next: Conjugate gradient
Up: ITERATIVE METHODS
Previous: Conditioning the gradient
Stanford Exploration Project
10/21/1998
![]() ,from parallel to perpendicular to the local contour line
for the next descent.
What if the final goal is at a 45
,from parallel to perpendicular to the local contour line
for the next descent.
What if the final goal is at a 45![]() angle to our path?
A 45
angle to our path?
A 45![]() turn cannot be made.
Instead of moving like a rain drop down the centerline of a rain gutter,
we move along a fine-toothed zigzag path,
crossing and recrossing the centerline.
The gentler the slope of the rain gutter,
the finer the teeth on the zigzag path.
1
turn cannot be made.
Instead of moving like a rain drop down the centerline of a rain gutter,
we move along a fine-toothed zigzag path,
crossing and recrossing the centerline.
The gentler the slope of the rain gutter,
the finer the teeth on the zigzag path.
1