




Next: Laying out a mesh
Up: FT AS AN INVERTIBLE
Previous: FT AS AN INVERTIBLE
The highest frequency
in equation (6),
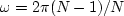 ,is almost
,is almost 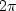 .This frequency is twice as high as the Nyquist frequency
.This frequency is twice as high as the Nyquist frequency  .The Nyquist frequency
is normally thought of as the ``highest possible'' frequency,
because
.The Nyquist frequency
is normally thought of as the ``highest possible'' frequency,
because 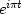 , for integer t,
plots as
, for integer t,
plots as 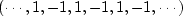 .The double Nyquist frequency function,
.The double Nyquist frequency function,
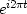 , for integer t,
plots as
, for integer t,
plots as 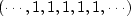 .So this frequency above the highest frequency is really zero frequency!
We need to recall that
.So this frequency above the highest frequency is really zero frequency!
We need to recall that 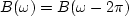 .Thus, all the frequencies near the upper end of the range (6)
are really small negative frequencies.
Negative frequencies on the interval
.Thus, all the frequencies near the upper end of the range (6)
are really small negative frequencies.
Negative frequencies on the interval 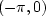 were moved to interval
were moved to interval 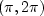 by the matrix form of Fourier summation.
by the matrix form of Fourier summation.
1





Next: Laying out a mesh
Up: FT AS AN INVERTIBLE
Previous: FT AS AN INVERTIBLE
Stanford Exploration Project
10/21/1998