




Next: Pseudounitary NMO with linear
Up: UNITARY OPERATORS
Previous: Meaning of B'B
A so-called unitary transformation 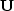 conserves energy.
In other words, if
conserves energy.
In other words, if 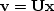 , then
, then 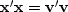 ,which requires
,which requires 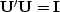 .Imagine an application
where the transformation seems as if it should not destroy information.
Can we arrange it to conserve energy?
The conventional inversion
.Imagine an application
where the transformation seems as if it should not destroy information.
Can we arrange it to conserve energy?
The conventional inversion
| 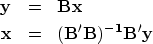 |
(27) |
| (28) |
can be verified by direct substitution.
Seeking a more symmetrical transformation
between 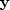 and
and  than the one above, we define
than the one above, we define
| 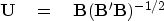 |
(29) |
and the transformation pair
| 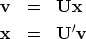 |
(30) |
| (31) |
where we can easily verify that
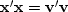 by direct substitution.
In practice, it would often be found that
by direct substitution.
In practice, it would often be found that  is
a satisfactory substitute for
is
a satisfactory substitute for 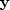 ,and further that the unitary property is often a significant advantage.
,and further that the unitary property is often a significant advantage.
Is the operator 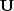 unitary?
It would not be unitary for NMO, because
equation (19) is not invertible.
Remember that we lost (x1,x2,x3,x4, and x5) in (17).
unitary?
It would not be unitary for NMO, because
equation (19) is not invertible.
Remember that we lost (x1,x2,x3,x4, and x5) in (17).
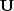 is unitary, however, except for lost points,
so we call it ``pseudounitary."
A trip into and back from the space of a pseudounitary operator
is like a pass through a bandpass filter.
Something is lost the first time,
but no more is lost if we do it again.
Thus,
is unitary, however, except for lost points,
so we call it ``pseudounitary."
A trip into and back from the space of a pseudounitary operator
is like a pass through a bandpass filter.
Something is lost the first time,
but no more is lost if we do it again.
Thus,
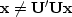 ,but
,but
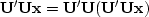 for any
for any  .Furthermore,
.Furthermore, 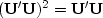 ,but
,but 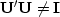 .In mathematics the operators
.In mathematics the operators
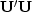 and
and
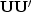 are called ``idempotent" operators.
Another example of an idempotent operator is that of subroutine
advance()
are called ``idempotent" operators.
Another example of an idempotent operator is that of subroutine
advance() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) 1
1





Next: Pseudounitary NMO with linear
Up: UNITARY OPERATORS
Previous: Meaning of B'B
Stanford Exploration Project
10/21/1998
![]() conserves energy.
In other words, if
conserves energy.
In other words, if ![]() , then
, then ![]() ,which requires
,which requires ![]() .Imagine an application
where the transformation seems as if it should not destroy information.
Can we arrange it to conserve energy?
The conventional inversion
.Imagine an application
where the transformation seems as if it should not destroy information.
Can we arrange it to conserve energy?
The conventional inversion
![]() unitary?
It would not be unitary for NMO, because
equation (19) is not invertible.
Remember that we lost (x1,x2,x3,x4, and x5) in (17).
unitary?
It would not be unitary for NMO, because
equation (19) is not invertible.
Remember that we lost (x1,x2,x3,x4, and x5) in (17).
![]() is unitary, however, except for lost points,
so we call it ``pseudounitary."
A trip into and back from the space of a pseudounitary operator
is like a pass through a bandpass filter.
Something is lost the first time,
but no more is lost if we do it again.
Thus,
is unitary, however, except for lost points,
so we call it ``pseudounitary."
A trip into and back from the space of a pseudounitary operator
is like a pass through a bandpass filter.
Something is lost the first time,
but no more is lost if we do it again.
Thus,
![]() ,but
,but
![]() for any
for any ![]() .Furthermore,
.Furthermore, ![]() ,but
,but ![]() .In mathematics the operators
.In mathematics the operators
![]() and
and
![]() are called ``idempotent" operators.
Another example of an idempotent operator is that of subroutine
advance()
are called ``idempotent" operators.
Another example of an idempotent operator is that of subroutine
advance() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) 1
1