To illustrate the concept, a program will be sketched that makes two images, first the usual image of the top side of the reflector, and second the image of the under side. The images may be viewed separately or summed.
The program makes the simplifying restriction on the velocity
that ![]() .Because of this assumption,
evanescent energy can be stored ``in place'' and ignored
until the return pass.
It is worth noting that the second pass is cheaper than the first pass
because the region in which evanescence never
occurred,
.Because of this assumption,
evanescent energy can be stored ``in place'' and ignored
until the return pass.
It is worth noting that the second pass is cheaper than the first pass
because the region in which evanescence never
occurred, ![]() , need not be
processed.
, need not be
processed.
# first pass of conventional phase-shift migration.FT[u(t,x)] For
,
, ...,
{ For all kx { Uimage
. For all
{
exp
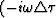
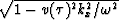
Uimage
Uimage
} } uimage
FT[Uimage
}
# Second pass for underside image. For,
,
, ..., 0 { For all kx { Dimage
. For all
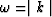
to
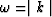
{ # The wave changes direction but so does
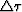
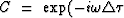
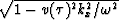
Dimage
Dimage
} } dimage
FT[Dimage
}