




Next: SIGNAL-NOISE DECOMPOSITION BY DIP
Up: Nonstationarity: patching
Previous: Which coefficients are really
Here we relate the basic theoretical statement
of geophysical inverse theory
to the basic theoretical statement
of separation of signals from noises.
A common form of linearized geophysical inverse theory is
inverse theory
| 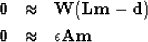 |
(7) |
| (8) |
We choose the operator 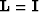 to be an identity
and we rename the model
to be an identity
and we rename the model 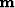 to be signal
to be signal  .Define noise by the decomposition of data into signal plus noise,
so
.Define noise by the decomposition of data into signal plus noise,
so
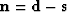 .Finally, let us rename the weighting (and filtering) operations
.Finally, let us rename the weighting (and filtering) operations
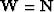 on the noise and
on the noise and
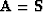 on the signal.
Thus the usual model fitting becomes
a fitting for signal-noise separation:
on the signal.
Thus the usual model fitting becomes
a fitting for signal-noise separation:
| 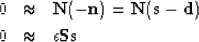 |
(9) |
| (10) |





Next: SIGNAL-NOISE DECOMPOSITION BY DIP
Up: Nonstationarity: patching
Previous: Which coefficients are really
Stanford Exploration Project
4/27/2004