![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) had a strong north-south tilt
which I
had a strong north-south tilt
which I![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) removed at the outset.
Figure
removed at the outset.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) gives our first view of altimetry data
(ocean height) from southeast of the island of
Madagascar.
gives our first view of altimetry data
(ocean height) from southeast of the island of
Madagascar.
A satellite points a radar at the ground and receives echos we investigate here. These echos are recorded only over the ocean. The echo tells the distance from the orbit to the ocean surface. After various corrections are made for earth and orbit ellipticities the residual shows tides, wind stress on the surface, and surprisingly a signal proportional to the depth of the water. Gravity of mountains on the water bottom pulls water towards them raising sea level there.
The raw data investigated here![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) had a strong north-south tilt
which I
had a strong north-south tilt
which I![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) removed at the outset.
Figure
removed at the outset.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) gives our first view of altimetry data
(ocean height) from southeast of the island of
Madagascar.
gives our first view of altimetry data
(ocean height) from southeast of the island of
Madagascar.
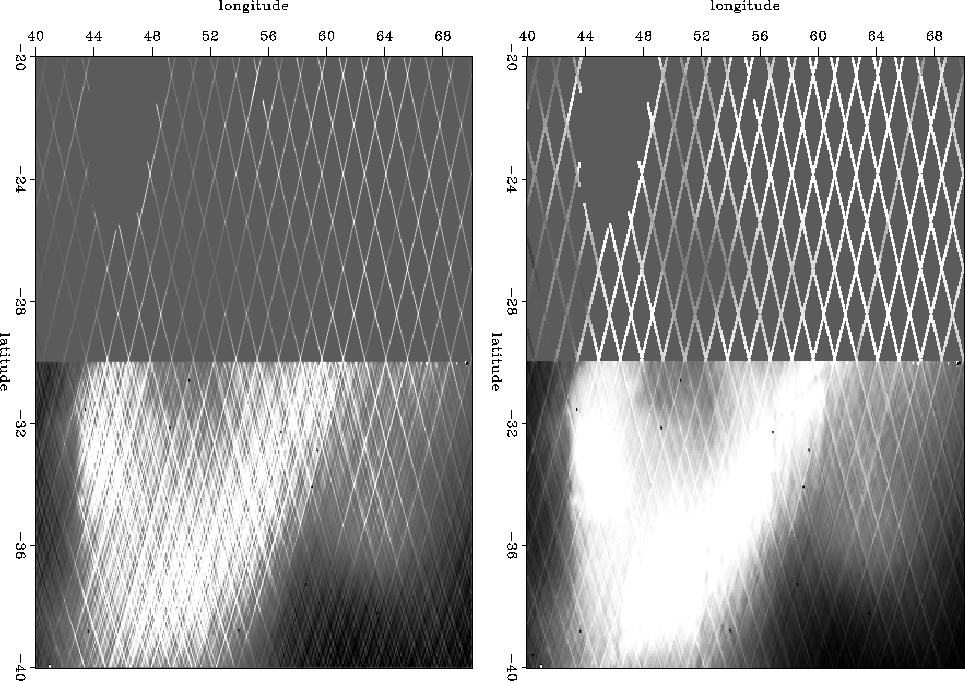 |
About all we can see is satellite tracks.
The satellite is in a circular polar orbit.
To us the sun seems to rotate east to west
as does the circular satellite orbit.
Consequently, when the satellite moves northward across the site
we get altitude measurements along a SE-NW line.
When it moves southward we get measurements along a NE-SW line.
This data is from the cold war era.
At that time dense data above the ![]() parallel was secret
although sparse data was available.
(The restriction had to do with precision guidance of missiles.
Would the missile hit the silo?
or miss it by enough to save the retaliation missile?)
parallel was secret
although sparse data was available.
(The restriction had to do with precision guidance of missiles.
Would the missile hit the silo?
or miss it by enough to save the retaliation missile?)
Here are some definitions:
Let components of ![]() be the data,
altitude measured along a satellite track.
The model space is
be the data,
altitude measured along a satellite track.
The model space is ![]() , altitude in the (x,y)-plane.
Let
, altitude in the (x,y)-plane.
Let ![]() denote the 2-D linear interpolation operator
from the track to the plane.
Let
denote the 2-D linear interpolation operator
from the track to the plane.
Let ![]() be the helix derivative,
a filter with response
be the helix derivative,
a filter with response ![]() .Except where otherwise noted,
the roughened image
.Except where otherwise noted,
the roughened image ![]() is the preconditioned variable
is the preconditioned variable
![]() .The derivative along a track in data space is
.The derivative along a track in data space is ![]() .A weighting function that vanishes when any filter hits a track end
or a bad data point is
.A weighting function that vanishes when any filter hits a track end
or a bad data point is ![]() .
.
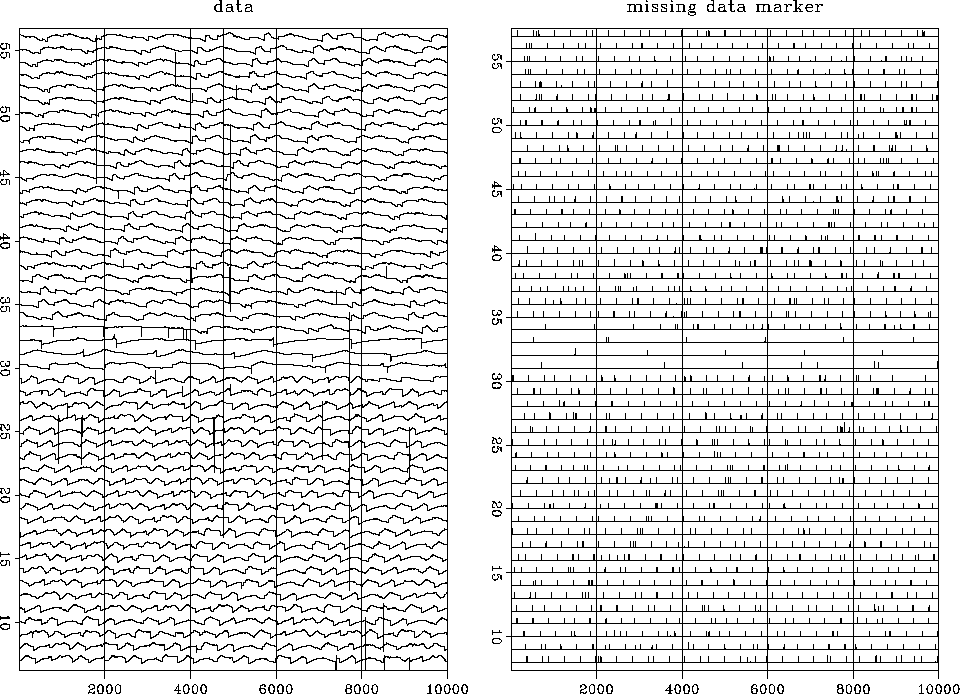 |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the entire data space,
over a half million data points (actually 537974).
Altitude is measured along many tracks across the image.
In Figure
shows the entire data space,
over a half million data points (actually 537974).
Altitude is measured along many tracks across the image.
In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the tracks are placed end-to-end,
so it is one long vector (displayed in about 50 signal rows).
A vector of equal length is the missing data marker vector.
This vector is filled with zeros everywhere except where
data is missing or known bad or known to be at the ends of the tracks.
The long tracks are the ones that are sparse in the north.
the tracks are placed end-to-end,
so it is one long vector (displayed in about 50 signal rows).
A vector of equal length is the missing data marker vector.
This vector is filled with zeros everywhere except where
data is missing or known bad or known to be at the ends of the tracks.
The long tracks are the ones that are sparse in the north.
|
jesse2
Figure 11 The roughened, normalized adjoint, |  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) brings this information into model space.
Applying the adjoint of the linear interpolation operator
brings this information into model space.
Applying the adjoint of the linear interpolation operator ![]() to the data
to the data ![]() gave our first image
gave our first image ![]() in model space in Figure
in model space in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The track noise was so large that roughening it made it worse.
A more inviting image arose when I normalized the image before roughening it.
Put a vector of all ones
.
The track noise was so large that roughening it made it worse.
A more inviting image arose when I normalized the image before roughening it.
Put a vector of all ones ![]() into the
adjoint of the linear interpolation operator
into the
adjoint of the linear interpolation operator ![]() .What comes out
.What comes out ![]() is roughly the number of data points landing in each pixel in model space.
More precisely, it is the sum of the linear interpolation weights.
This then, if it is not zero, is used as a divisor.
The division accounts for several tracks contributing to one pixel.
In matrix formalism this image is
is roughly the number of data points landing in each pixel in model space.
More precisely, it is the sum of the linear interpolation weights.
This then, if it is not zero, is used as a divisor.
The division accounts for several tracks contributing to one pixel.
In matrix formalism this image is
![]() .In Figure
.In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) this image is roughened
with the helix derivative
this image is roughened
with the helix derivative ![]() .
.
 |
There is a simple way here to make a nice image--roughen
along data tracks.
This is done in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The result is two attractive images, one for each track direction.
Unfortunately, there is no simple relationship between the two images.
We cannot simply add them because the shadows go in different directions.
Notice also that each image has noticeable tracks that we would
like to suppress further.
.
The result is two attractive images, one for each track direction.
Unfortunately, there is no simple relationship between the two images.
We cannot simply add them because the shadows go in different directions.
Notice also that each image has noticeable tracks that we would
like to suppress further.
A geological side note: The strongest line, the line that marches along the image from southwest to northeast is a sea-floor spreading axis. Magma emerges along this line as a source growing plates that are spreading apart. Here the spreading is in the north-south direction. The many vertical lines in the image are called ``transform faults''.
Fortunately, we know how to merge the data.
The basic trick is to form the track derivative
not on the data (which would falsify it)
but on the residual which
(in Fourier space) can be understood as
choosing a different weighting function for the statistics.
A track derivative on the residual is actually two track derivatives,
one on the observed data, the other on the modeled data.
Both data sets are changed in the same way.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result.
shows the result.
 |
The altitude function remains too smooth for nice viewing
by variable brightness,
but roughening it with ![]() makes an attractive image
showing, in the south, no visible tracks.
makes an attractive image
showing, in the south, no visible tracks.
The north is another story. We would like the sparse northern tracks to contribute to our viewing pleasure. We would like them to contribute to a northern image of the earth, not to an image of the data acquisition footprint.
 |
This begins to happen in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The process of fitting data by choosing an altitude function
.
The process of fitting data by choosing an altitude function ![]() would normally include some regularization (model styling),
such as
would normally include some regularization (model styling),
such as
![]() .Instead we adopt the usual trick
of changing to preconditioning variables,
in this case
.Instead we adopt the usual trick
of changing to preconditioning variables,
in this case ![]() .As we iterate with the variable
.As we iterate with the variable ![]() we watch the images
of
we watch the images
of ![]() and
and ![]() and quit either when we are tired,
or more hopefully, when we are best satisified with the image.
This subjective choice is rather like choosing the
and quit either when we are tired,
or more hopefully, when we are best satisified with the image.
This subjective choice is rather like choosing the ![]() that is the balance between data fitting goals and model styling goals.
The result
in Figure
that is the balance between data fitting goals and model styling goals.
The result
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is pleasing.
We have begun building topography in the north that continues
in a consistant way with what is in the south.
Unfortunately, this topography does fade out rather quickly
as we get off the data acquisition tracks.
is pleasing.
We have begun building topography in the north that continues
in a consistant way with what is in the south.
Unfortunately, this topography does fade out rather quickly
as we get off the data acquisition tracks.
If we have reason to suspect that the geological style north of
the 30th parallel matches that south of it
(the stationarity assumption) we can compute a PEF on the south side
and use it for interpolation on the north side.
This is done in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
 |
This is about as good as we are going to get. Our fractured ridge continues nicely into the north. Unfortunately, we have imprinted the fractured ridge texture all over the northern space, but that's the price we must pay for relying on the stationarity assumption.
The fitting residuals
are shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
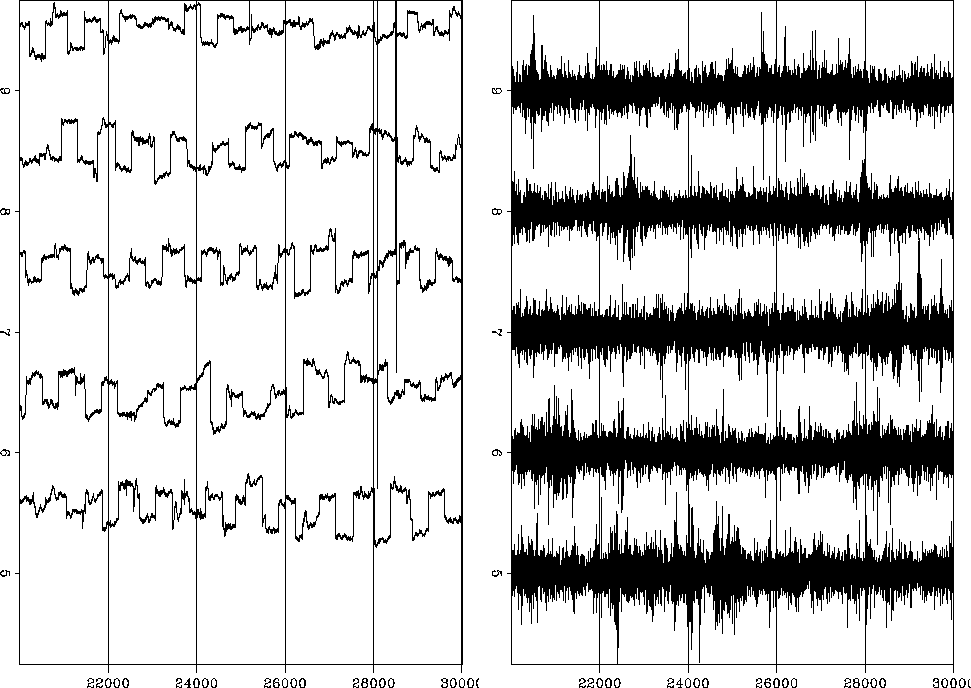 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Left is physical residual
.
Left is physical residual
The physical altitude residuals tend to be rectangles,
each the duration of a track.
While the satellite is overflying other earth locations the ocean surface
is changing its altitude.
The fitting residuals (right side) are very fuzzy.
They appear to be ``white'', though with ten thousand points
crammed onto a line a couple inches long, we cannot be certain.
We could inspect this further.
If the residuals turn out to be significantly non-white,
we might do better to change ![]() to a PEF along the track.
to a PEF along the track.