




Next: MEDIAN BINNING
Up: NOISE BURSTS
Previous: De-spiking with median smoothing
Most signals are smooth, but running medians assume they have no curvature.
An alternate expression of this assumption is that the signal
has minimal curvature
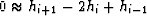 ;in other words,
;in other words,
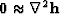 .Thus we propose to create the cleaned-up data
.Thus we propose to create the cleaned-up data 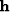 from the observed data
from the observed data 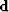 with the fitting problem
with the fitting problem
| 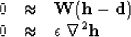 |
(18) |
where 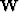 is a diagonal matrix with weights sprinkled along the diagonal,
and where
is a diagonal matrix with weights sprinkled along the diagonal,
and where 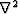 is a matrix
with a roughener like (1,-2,1) distributed along the diagonal.
This is shown in Figure
is a matrix
with a roughener like (1,-2,1) distributed along the diagonal.
This is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with
with 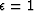 .Experience showed similar performances
for
.Experience showed similar performances
for 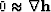 and
and 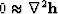 .Better results, however, will be found later in Figure
.Better results, however, will be found later in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
where the
,
where the 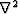 operator is replaced
by an operator designed to predict this very predictable signal.
operator is replaced
by an operator designed to predict this very predictable signal.





Next: MEDIAN BINNING
Up: NOISE BURSTS
Previous: De-spiking with median smoothing
Stanford Exploration Project
4/27/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with
with ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
where the
,
where the