




Next: Confusing terminology for data
Up: MULTIVARIATE SPECTRUM
Previous: MULTIVARIATE SPECTRUM
Least-squares problems often present themselves as fitting goals such as
| 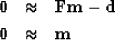 |
(58) |
| (59) |
To balance our possibly contradictory goals we need weighting functions.
The quadratic form that we should minimize is
| 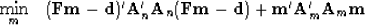 |
(60) |
where 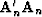 is the inverse multivariate spectrum of the noise
(data-space residuals) and
is the inverse multivariate spectrum of the noise
(data-space residuals) and
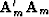 is the inverse multivariate spectrum of the model.
In other words,
is the inverse multivariate spectrum of the model.
In other words,
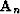 is a leveler on the data fitting error and
is a leveler on the data fitting error and
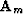 is a leveler on the model.
There is a curious unresolved issue:
What is the most suitable constant scaling ratio
of
is a leveler on the model.
There is a curious unresolved issue:
What is the most suitable constant scaling ratio
of 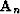 to
to 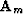 ?
?





Next: Confusing terminology for data
Up: MULTIVARIATE SPECTRUM
Previous: MULTIVARIATE SPECTRUM
Stanford Exploration Project
4/27/2004