Null space and iterative methods

In applications where we fit $\bold d \approx\bold F \bold x$,there might exist a vector (or a family of vectors) defined by the condition $\bold 0 =\bold F \bold x_{\rm null}$.This family is called a null space. For example, if the operator $\bold F$ is a time derivative, then the null space is the constant function; if the operator is a second derivative, then the null space has two components, a constant function and a linear function, or combinations of them. The null space is a family of model components that have no effect on the data.

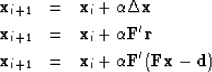
When we use the steepest-descent method, we iteratively find solutions by this updating:

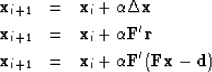$$\begin{eqnarray} \bold x_{i+1} &=& \bold x_i + \alpha \Delta \bold x \\ \bold x_... ...d x_{i+1} &=& \bold x_i + \alpha \bold F'(\bold F\bold x -\bold d)\end{eqnarray}$$ (50) (51) (52)

After we have iterated to convergence, the gradient $\Delta \bold x$ vanishes as does $\bold F'(\bold F\bold x -\bold d)$.Thus, an iterative solver gets the same solution as the long-winded theory leading to equation (27).

Suppose that by adding a huge amount of $\bold x_{\rm null}$,we now change $\bold x$and continue iterating. Notice that $\Delta \bold x$ remains zero because $\bold F \bold x_{\rm null}$ vanishes. Thus we conclude that any null space in the initial guess $\bold x_0$will remain there unaffected by the gradient-descent process.

Linear algebra theory enables us to dig up the entire null space should we so desire. On the other hand, the computer demands might be vast. Even the memory for holding the many $\bold x$ vectors could be prohibitive. A much simpler and more practical goal is to find out if the null space has any members, and if so, to view some of them. To try to see a member of the null space, we take two starting guesses and we run our iterative solver for each of them. If the two solutions, $\bold x_1$ and $\bold x_2$,are the same, there is no null space. If the solutions differ, the difference is a member of the null space. Let us see why: Suppose after iterating to minimum residual we find

$$\begin{eqnarray} \bold r_1 &=& \bold F\bold x_1 - \bold d \\ \bold r_2 &=& \bold F\bold x_2 - \bold d \end{eqnarray}$$ (53) (54)

We know that the residual squared is a convex quadratic function of the unknown $\bold x$.Mathematically that means the minimum value is unique, so $\bold r_1 =\bold r_2$.Subtracting we find $0=\bold r_1-\bold r_2 =\bold F(\bold x_1-\bold x_2)$proving that $\bold x_1-\bold x_2$ is a model in the null space. Adding $\bold x_1-\bold x_2$ to any to any model $\bold x$will not change the theoretical data. Are you having trouble visualizing $\bold r$ being unique, but $\bold x$ not being unique? Imagine that $\bold r$happens to be independent of one of the components of $\bold x$.That component is nonunique. More generally, it is some linear combination of components of $\bold x$that $\bold r$ is independent of.

A practical way to learn about the existence of null spaces and their general appearance is simply to try gradient-descent methods beginning from various different starting guesses.

``Did I fail to run my iterative solver long enough?'' is a question you might have. If two residuals from two starting solutions are not equal, $\bold r_1 \ne \bold r_2$,then you should be running your solver through more iterations.

If two different starting solutions produce two different residuals, then you didn't run your solver through enough iterations.