Nearest-neighbor coordinates

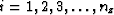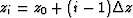nearest neighbor coordinates In describing physical processes, we often either specify models as values given on a uniform mesh or we record data on a uniform mesh. Typically we have a function f of time t or depth z and we represent it by f(iz) corresponding to f(z_i) for $i=1,2,3,\ldots, n_z$where $z_i = z_0+ (i-1)\Delta z$.We sometimes need to handle depth as an integer counting variable i and we sometimes need to handle it as a floating-point variable z. Conversion from the counting variable to the floating-point variable is exact and is often seen in a computer idiom such as either of

            do iz= 1, nz {   z = z0 + (iz-1) * dz 
            do i3= 1, n3 {  x3 = o3 + (i3-1) * d3

The reverse conversion from the floating-point variable to the counting variable is inexact. The easiest thing is to place it at the nearest neighbor. This is done by solving for iz, then adding one half, and then rounding down to the nearest integer. The familiar computer idioms are:

        iz =  .5 + 1 + ( z - z0) / dz
        iz = 1.5 +     ( z - z0) / dz
        i3 = 1.5 +     (x3 - o3) / d3

A small warning is in order: People generally use positive counting variables. If you also include negative ones, then to get the nearest integer, you should do your rounding with the Fortran function NINT().