Zero padding is the transpose of truncation

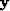Surrounding a dataset by zeros (zero padding) is adjoint to throwing away the extended data (truncation). Let us see why this is so. Set a signal in a vector $\bold x$, and then to make a longer vector $\bold y$,add some zeros at the end of $\bold x$.This zero padding can be regarded as the matrix multiplication

$$\bold y\eq \left[ \begin{array} {c} \bold I \\ \bold 0 \end{array} \right] \ \bold x$$ (11)

The matrix is simply an identity matrix 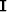$\bold I$above a zero matrix $\bold 0$.To find the transpose to zero-padding, we now transpose the matrix and do another matrix multiply:

$$\tilde {\bold x} \eq \left[ \begin{array} {cc} \bold I & \bold 0 \end{array} \right] \ \bold y$$ (12)

So the transpose operation to zero padding data is simply truncating the data back to its original length. Module zpad1 below pads zeros on both ends of its input. Modules for two- and three-dimensional padding are in the library named zpad2() and zpad3(). zpad1zero pad 1-D